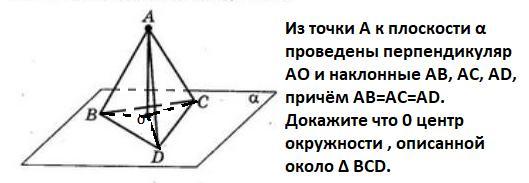
ПОМОГИТЕ ПОЖАЛУЙСТА.!!! СРОЧНО!!! Из точки А к плоскости альфа проведены перпендикуляр AO и наклонные AB, AC, AD, причëм AB=AC=AD. Докажите что 0 центр окружности , описанной около треугольника BCD.
Приложения:

Ответы
Ответ дал:
1
Из точки А к плоскости α проведены перпендикуляр AO и наклонные AB, AC, AD, причëм AB=AC=AD. Докажите что 0 центр окружности , описанной около Δ BCD.
Объяснение:
Т.к. АО перпендикуляр к плоскости α, то АО перпендикулярен любой прямой , лежащей в плоскости α ⇒∠АВО=∠АСО=∠АDO=90°.
Поэтому прямоугольные ΔАВО=ΔАСО=ΔАDO по гипотенузе (AB=AC=AD) и катету (АО-общий).Значит соответственные элементы равны ⇒ ОВ=ОС=ОD ⇒O-равноудалена от вершин ΔВСD ⇒O-центр описанной окружности.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад