Пожалуйста сделайте на листочке и отправьте мне докажите что при всех значениях в не рано
Приложения:
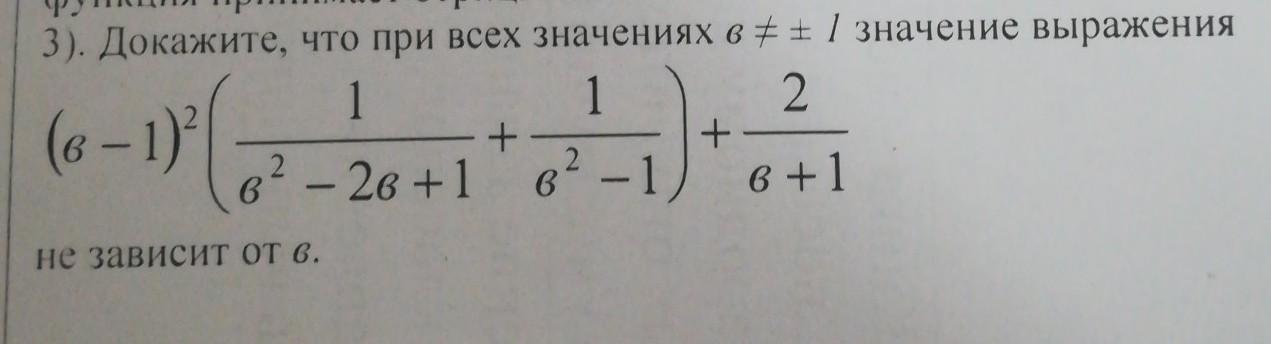
Ответы
Ответ дал:
1
Ответ:
объяснения на фото .
Объяснение:
Приложения:
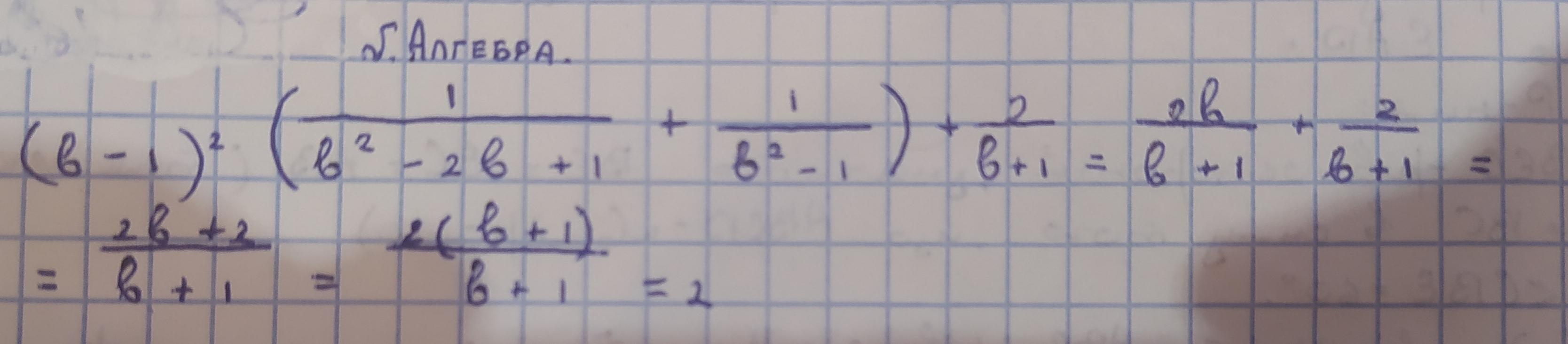
Ответ дал:
1
В ответе не содержится переменная b , значит значение выражения не зависит от b .
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад