Найдите периметр ромба, если его диагонали равны: 1)12 см и 16 см; 2) 14 см и 48 см. помогите пожалуйста даю много баллов
muhammadievbehruz302:
помогите
Ответы
Ответ дал:
13
Нужно знать:
1. Ромб - это праллелограмм, у которого все строны равны.
2. Диагонали ромба перпендикулярны и точкой пересечения делятся пополам.
3. Периметр ромба находят по формуле Р = 4а, где а - строна ромба.
Поэтому:
см. рисунок.
Пусть дан ромб, АС и ВD - диагонали.
Тогда, т.к. АС ⊥ ВD, то ΔВОС - прямоугольный, ВО = ВD/2, ОС = АС/2.
По теореме Пифагора ВС² = ОС² + ВО².
1) АС = 12 см, ВD = 16 см, тогда ВО = 8 см, ОС = 6 см,
ВС² = 6² + 8² = 36 + 64 = 100, откуда ВС = 10 см.
Р = 4 · 10 = 40 (см).
2) АС = 14 см, ВD = 48 см, тогда ВО = 24 см, ОС = 7 см,
ВС² = 7² + 24² = 49 + 576 = 625, откуда ВС = 25 см.
Р = 4 · 25 = 100 (см).
Ответ: 1) 40 см; 2) 100 см.
Приложения:
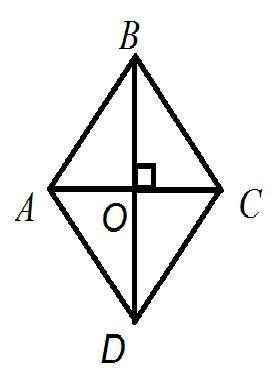
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад