Question

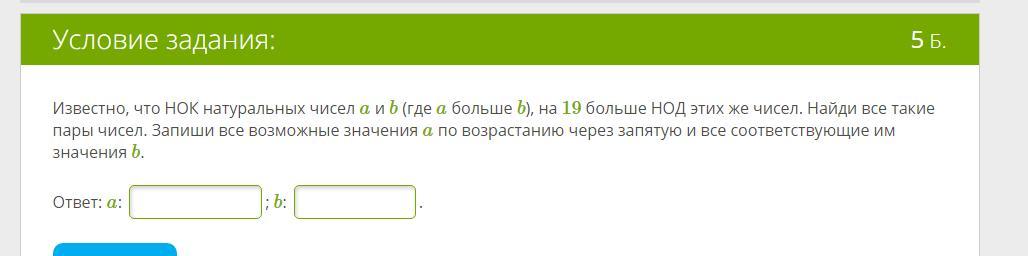
Известно, что НОК натуральных чисел a и b (где a больше b), на 19 больше НОД этих же чисел. Найди все такие пары чисел. Запиши все возможные значения a по возрастанию через запятую и все соответствующие им значения b.

Answer 1

Ответ:

Пусть НОК = К, НОД = D, тогда, по определению

а = К*A, b = K*В, D = K*A*B (где А, В - некие натуральные взаимно простые числа)

K*A*B - K = 29 по условию => К*(А*В-1) = 29 (1)

29 - простое число, равное произведению двух множителей. Значит, возможны два случая:

1) К=29, A*B-1=1 => A*B=2 => A=2, B =1 (так как а>b). Отсюда находим первую пару: а = 58, b = 29

2) К=1, А*В-1=29 => A*B=30=2*3*5. Выпишем все пары делителей, как возможные варианты (помним, что a>b):

А=30 В=1

А=15 В=2

А=10 В=3

А=6 В=5

Так как К = 1, то это остальные пары a,b

Пошаговое объяснение: