Question

Решите задачу.

Дано:

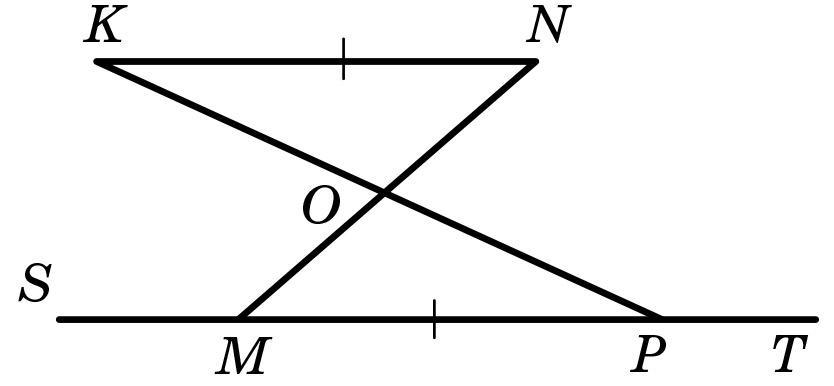
KN параллельна MP, KN = MP.

∠KNO = 43°.

∠OCD = 32°.

Найдите ∠SMO и ∠OPT

Answer 1

Объяснение:

Углы вертикальные - они равны;

KN параллельно MP =>

∠KNO = ∠OMP (т.к. накрест лежащие) =>

∠OPM = ∠OKN (по сумме углов в треугольнике или как накрест лежащие) =>

∆OMP = ∆KON (по стороне и двум прилежащим к ней углам).

Уголы SMO и OMP смежные, как и OPT и OPM, значит искомые углы можно найти следующим способом:

∠SMO = 180° - 43° = 137°

∠OPT = 180° - 32° = 148°

Ответ: 137°, 148° .