Question

3. Окружность, вписанная в треугольник ABC, касается стороны ВС в точке D. Докажите, что если отрезок AD — медиана треугольника, то AB = AC.
С РИСУНКОМ. отдаю все баллы!!!​

Answer 1

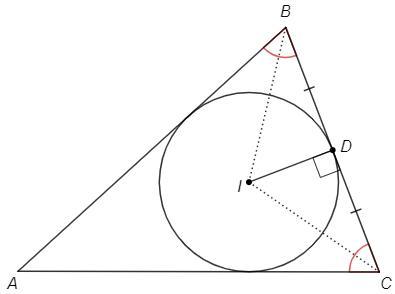
Центр вписанной окружности (I) - точка пересечения биссектрис.

Радиус в точку касания перпендикулярен касательной, ID⊥BC.

ID - высота и медиана => △BIC - равнобедренный.

IBC=ICB => B/2 =C/2 => B=C => △BAC - равнобедренный, AB=AC