Question

Помогите пожалуйста с алгеброй.СРОЧНО!!!!

Answer 1

Вот) Больше номеров к сожалению не сделаю

Answer 2

Вариант 11

1.

а) $sin(\frac{5\pi }{12})cos(\frac{\pi }{12})+sin(\frac{\pi }{12} )cos(\frac{5\pi }{12}) = sin(\frac{5\pi }{12} + \frac{\pi }{12}) = sin(\frac{6\pi }{12}) = sin(\frac{\pi }{2}) = 1$

б) cos78°cos12° - sin78°sin12° = cos(78°+12°) = cos(90°) = 0

в) sin15° + sin45°/cos15° = sin15° + √2/2 / cos15° = 2sin15°+√2/2 / cos15° = 2sin15°+√2/2cos15° = 2sin(45°-30°)+√2/2cos(45°-30°) = 2(sin45°cos30°-cos45°sin30°)+√2 / 2(cos45°cos30°+sin45°sin30°) = 2(√2/2 × √3/2 - √2/2 × 1/2)+√2/2(√2/2 × √3/2 + √2/2 × 1/2) = 2(√6/4 - √2/4)+√2 / 2(√6/4 + √2/4) = 2 × √6-√2/4 + √2 / 2 × √6+√2/4 = √6-√2/2 + √2 /√6+√2/2 = √6-√2+2√2/2 / √6+√2/2 = √6+√2/2 / √6+√2/2 = 1

2.

а) $\frac{\sqrt{2} }{2}cos\alpha - sin(\frac{\pi }{4}+\alpha ) = \frac{\sqrt{2} cos\alpha }{2} - (sin\frac{\pi }{4} cos\alpha + cos\frac{\pi }{4} sin\alpha ) = \frac{\sqrt{2} cos\alpha }{2} -(\frac{\sqrt{2} }{2}cos\alpha + \frac{\sqrt{2} }{2} sin\alpha ) = \frac{\sqrt{2} cos\alpha }{2} - (\frac{\sqrt{2} cos\alpha }{2} + \frac{\sqrt{2} sin\alpha }{2}) = \frac{\sqrt{2} cos\alpha }{2} - \frac{\sqrt{2}cos\alpha + \sqrt{2} sin\alpha }{2} = \frac{\sqrt{2}cos\alpha -(\sqrt{2}cos\alpha +\sqrt{2}sin\alpha)}{2} =$$= \frac{\sqrt{2}cos\alpha -\sqrt{2}cos\alpha-\sqrt{2}sin\alpha}{2} = \frac{-\sqrt{2}sin\alpha}{2} = - \frac{\sqrt{2}sin\alpha}{2}$

б)$\frac{1-cos2\alpha }{sin2\alpha } = tg(\frac{2\alpha }{\alpha }) = tg\alpha$

в) $1-(cos\alpha * tg\alpha)^{2} = 1 - (cos\alpha * \frac{sin\alpha }{cos\alpha })^{2} = 1-sin^{2}\alpha = cos^{2}\alpha$

г)$\frac{sin(-\alpha) + cos(\pi +\alpha )}{1+2cos(\frac{\pi }{2}+\alpha )cos(-\alpha) } = \frac{-sin\alpha - cos\alpha }{1+2(-sin\alpha )cos(-\alpha)} = \frac{-sin\alpha - cos\alpha }{1-2sin\alpha *cos\alpha}=\frac{-sin\alpha - cos\alpha }{1-sin2\alpha }=-\frac{sin\alpha +cos\alpha }{1-sin2\alpha }$

3. Воспользуемся формулой тригонометрического тождества:

sin²α + cos²α = 1

так как π<α<3π/2, то есть α в 3 четверти, косинус в третьей четверти имеет знак -, то  получается:

cosα = -√1-sin²α = -√1-(-0,6)² = -√1-0,36 = -√0,64 = -0,8

Найдем сначала cos2α по формуле кратных аргументов:

cos2α = cos²α - sin²α

cos2α = (-0,8)² - (-0,6)² = 0,64 - 0,36 = 0,28

Теперь находим $tg(\frac{\pi }{3} - \alpha )$ по такой формуле:

$tg(\frac{\pi }{3} - \alpha ) = \frac{tg\frac{\pi }{3}-tg\alpha }{1+tg\frac{\pi }{3}tg\alpha } = \frac{\sqrt{3}-tg\alpha }{1+\sqrt{3}*tg\alpha}$

Нам не известно tg α, значит нам надо найти tg α и потом $tg(\frac{\pi }{3} - \alpha )$:

$tg\alpha = \frac{sin\alpha }{cos\alpha } = \frac{-0,6}{-0,8} = 0,75$

$tg(\frac{\pi }{3} - \alpha ) = \frac{\sqrt{3}-0,75}{1+\sqrt{3}*0,75 } = \frac{1,73-0,75}{1+1,73*0,75} = \frac{0,98}{1+1,2975} = \frac{0,98}{2,2975} = 0,43$

Ответ: cos2α = 0,28;   tg(π/3 - α) ≈ 0,43

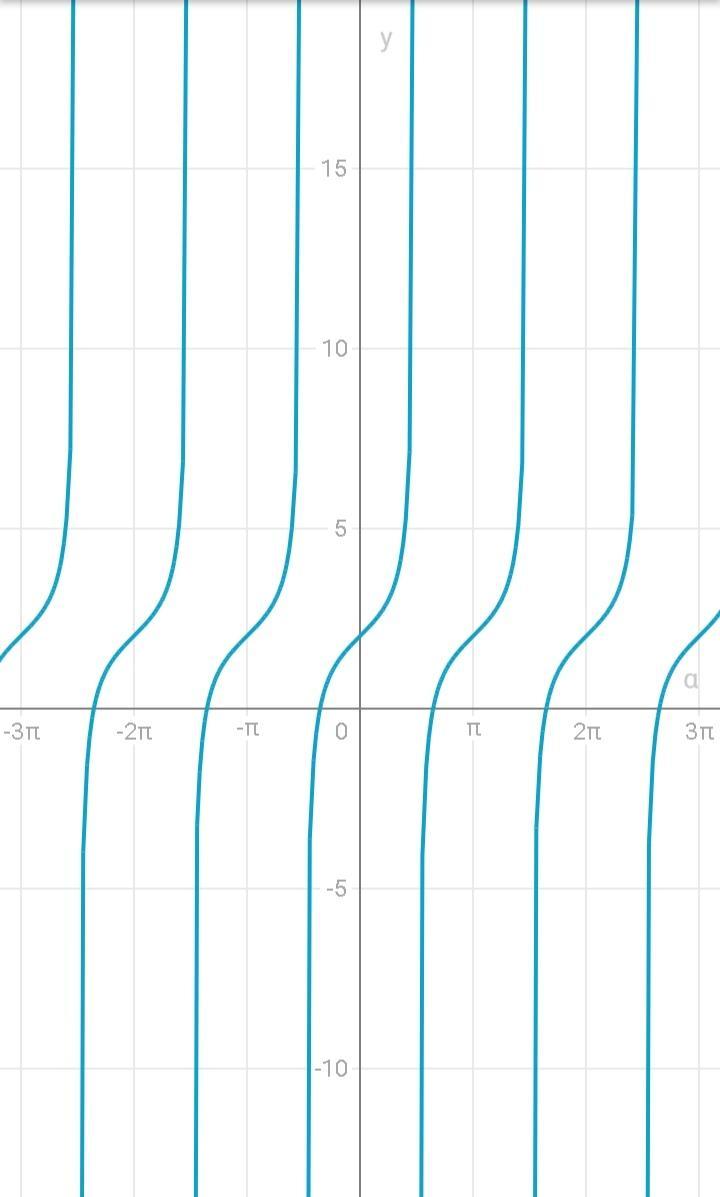
4. Построение этого графика показано внизу график, и его данные:↓