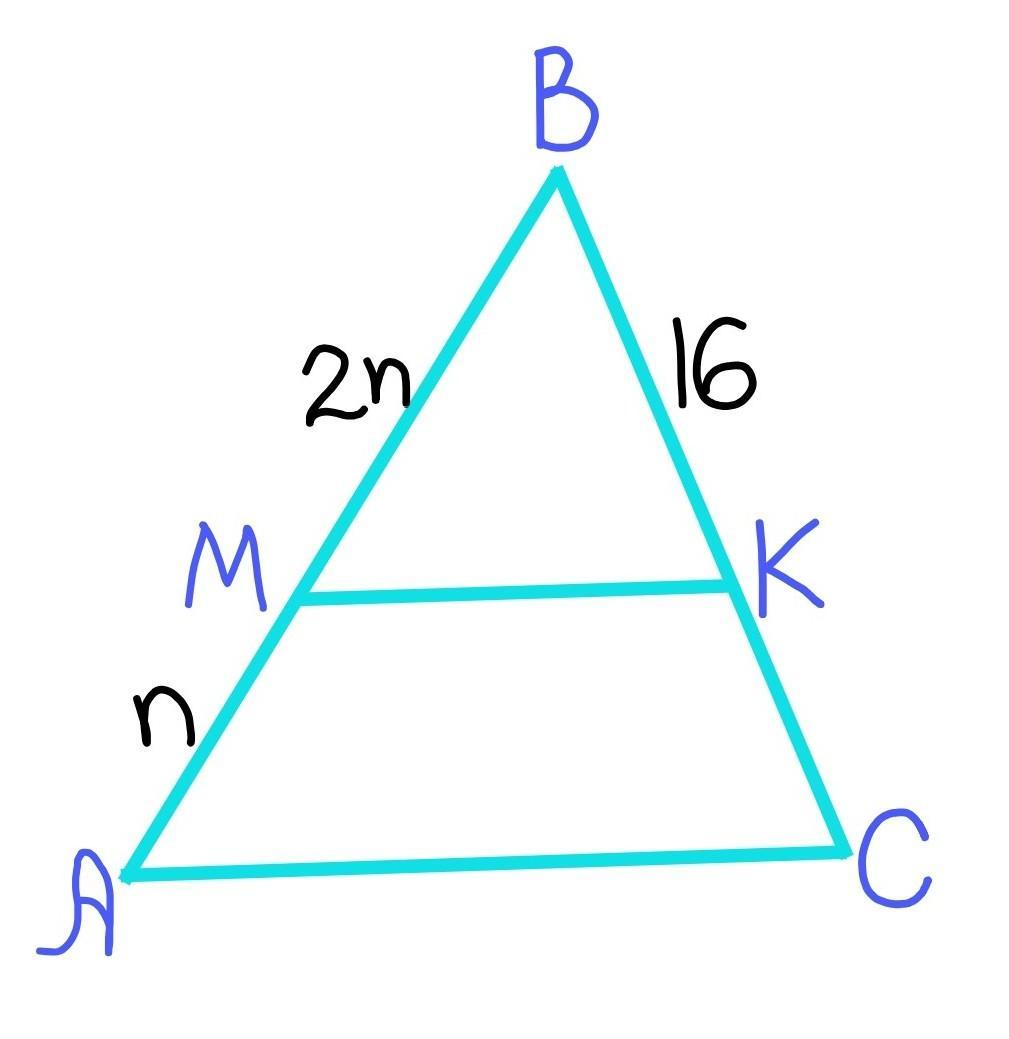
Решить задачу: дан треугольник АВС, МК ║ АС (М лежит на АВ, К лежит на ВС), ВК=16 см, отрезок ВМ в 2 раза больше отрезка АМ. Определите сторону ВС.
.
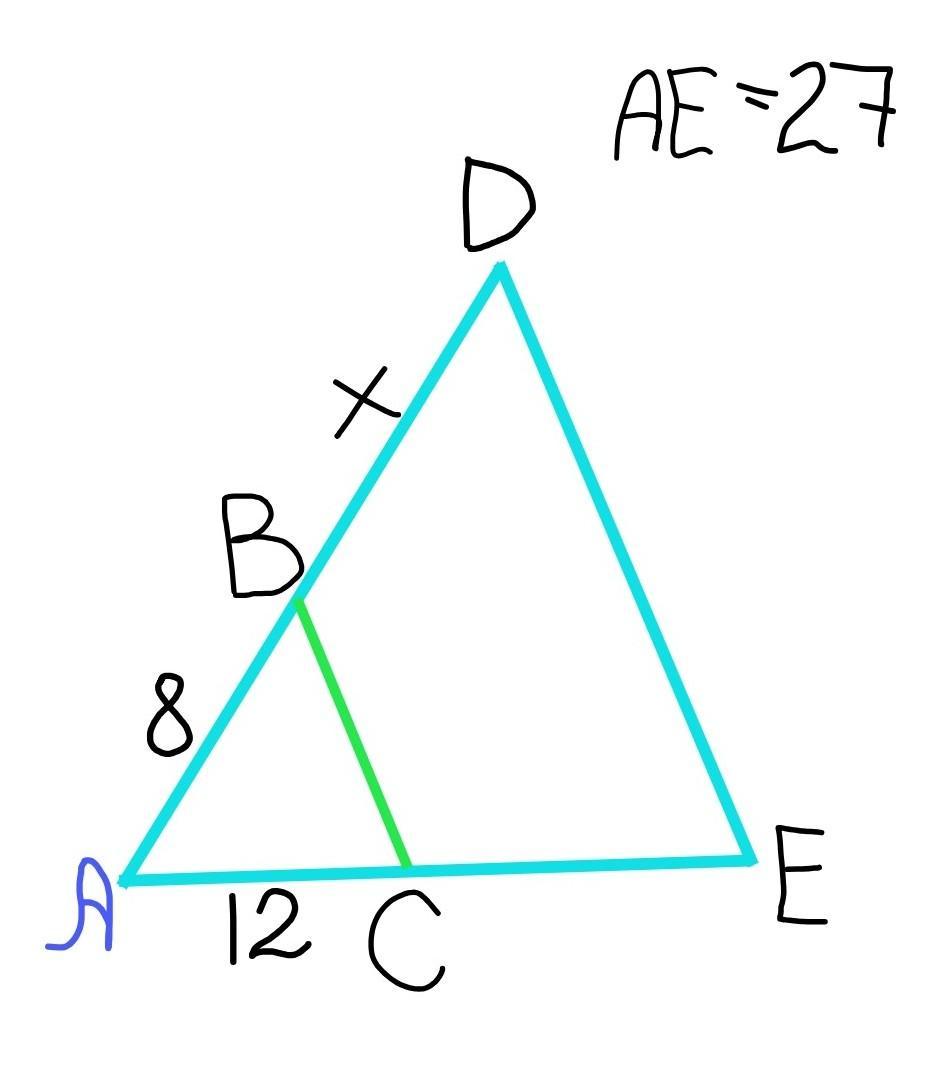
Решить задачу: дан треугольник АДЕ, ВС║ДЕ (В лежит на АД, С лежит на АЕ). Найдите ВД, если АВ=8, АС=12, АЕ=27.
orjabinina:
1) ВС=16+8=....
2) СЕ=15 , ВД=10
Ответы
Ответ дал:
3
№1
Так как МК//АС по условию, то угол BMK=угол ВАС как соответственные при параллельных прямых МК и АС и секущей АВ.
Угол АВС – общий.
Тогда ∆МВК~∆АВС по двум углам.
Стороны подобных треугольников пропорциональны, то есть:
МВ/АВ=ВК/ВС
МВ/(АМ+ВМ)=ВК/BC
Пусть АС=n, тогда МВ=2n
2n/(n+2n)=16/BC
2n/3n=16/BC
2/3=16/BC
16*3=2*BC
48=2*BC
BC=24 см
Ответ: 24 см.
№2
Так как ВС//DE по условию, то угол АСВ=угол АЕD как соответственные при параллельных прямых ВС и DE и секущей АЕ.
Угол DAE – общий.
Тогда ∆АСВ~∆АЕD по двум углам.
Стороны подобных треугольников пропорциональны, то есть:
АВ/АС=АD/AE
8/12=AD/27
2/3=AD/27
3*AD=27*2
3*AD=54
AD=18 см
ВD=AD–AB=18–8=10 см
Ответ: 10 см
Приложения:
Значёк / Это параллельно?
// да
/ – дробь
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад