Question

даю 40 баллов!) помогите пожалуйста

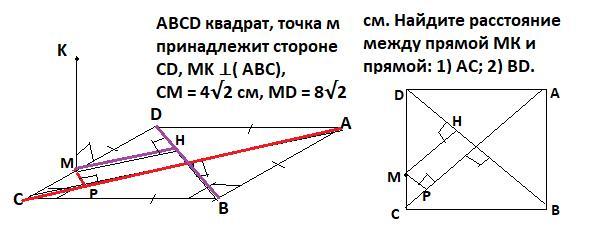
ABCD квадрат, точка м належить стороні СD,
MK L (ABC), см = 4√2 см, MD = 8√2 см. Знайдіть відстань
між прямою МК і прямою:
1) АС; 2) BD.​

Answer 1

ABCD квадрат, точка м принадлежит стороне СD, MK ⊥( ABC), СМ = 4√2 см, MD = 8√2 см. Найдите расстояние между прямой МК и прямой: 1) АС; 2) BD.​

Объяснение:

Расстояние между двумя прямыми - это наименьшее расстояние между любыми 2-я точками, лежащими на линии. Или между точкой лежащей на прямой с другой параллельной прямой.

1) Пусть МР⊥АС, тогда расстоянием между МК и АС будет отрезок МР. ΔСМР подобен ΔCDH по 2-м углам : ∠С-общий , ∠СРМ=∠COD=90° по св. диагоналей⇒ сходственные стороны пропорциональны   $\frac{MP}{OD} =\frac{CM}{CD}$ . Отрезок CD=4√2+8√2=12√2(cм) .

Найдем диагональ квадрата по т. Пифагора АС=√((12√2)²+(12√2)²)=24 ( см). Тогда половина диагонали DO=12 см.

$\frac{MP}{12} =\frac{4\sqrt{2} }{12\sqrt{} 2}$ , МР=4 см.

2) Пусть МН⊥BD, тогда расстоянием между МH и BD будет отрезок МH. Т.к. MD=2/3*DC,   $\frac{MH}{OC} =\frac{2}{3}$ ,

$\frac{MH}{12} =\frac{2}{3}$ , МH=8 см.