СРОЧНО! 70 БАЛЛОВ!
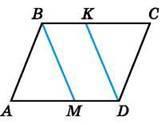
На сторонах AD и BC параллелограмма ABCD отмечены точки M и K так, что ∠ABM = ∠CDK. Докажи, что BMDK - параллелограмм.
Приложения:
Ответы
Ответ дал:
2
Ответ:
Объяснение:
В параллелограмме противоположные углы равны.
∠АВС=∠ADC (по свойству), ∠ABM=∠CDK (по условию) ⇒ ∡KBD=∡MDK (разница одинаковых углов, противоположные углы B и D четырехугольника BMDK);
ΔABM=ΔCDK (по стороне и прилегающей к ней углам);
∡BMK=∡BKD (смежные с равными углами ΔABM и ΔCDK, противоположные углы М и К четырехугольника BMDK);
Противоположные углы B,D и М,К четырехугольника BMDK равны ⇒ BMDK параллелограмм.
777wow:
Спасибо, добрый человек)))
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад