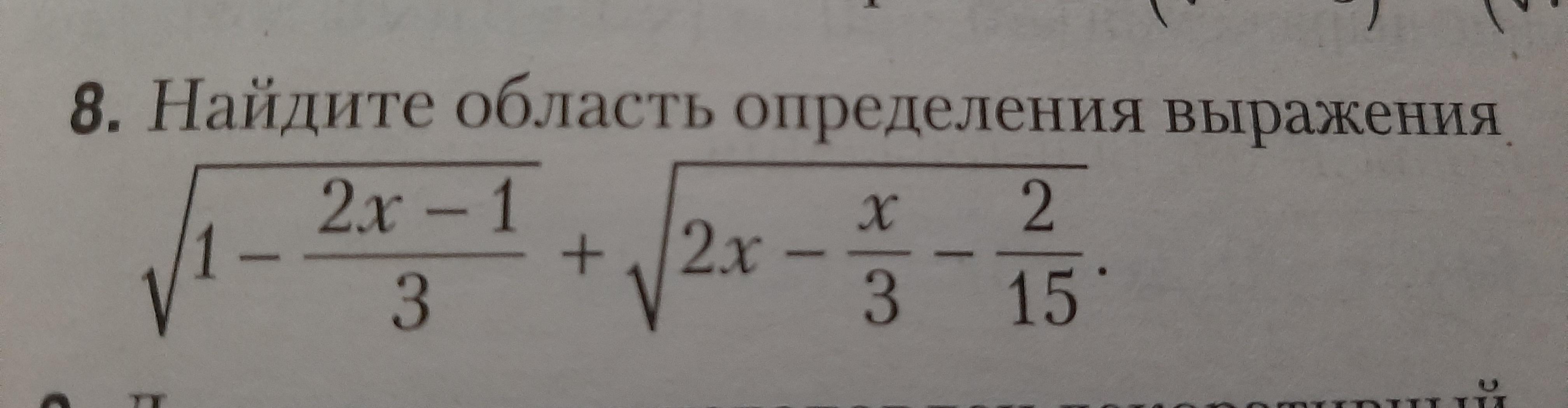Ответы
Ответ дал:
1
Значение корня из отрицательного числа не определено.
Поэтому нам надо выбрать такие значения x, при которых выражения под корнями будет не меньше нуля.
Для первого корня:
Для второго корня:
Чтобы выражение, содержащее несколько корней, имело определённое значение, нужно, чтобы все эти корни тоже имели определённое значение.
Таким образом, область определения выражения будет такой:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад