40 баллов!
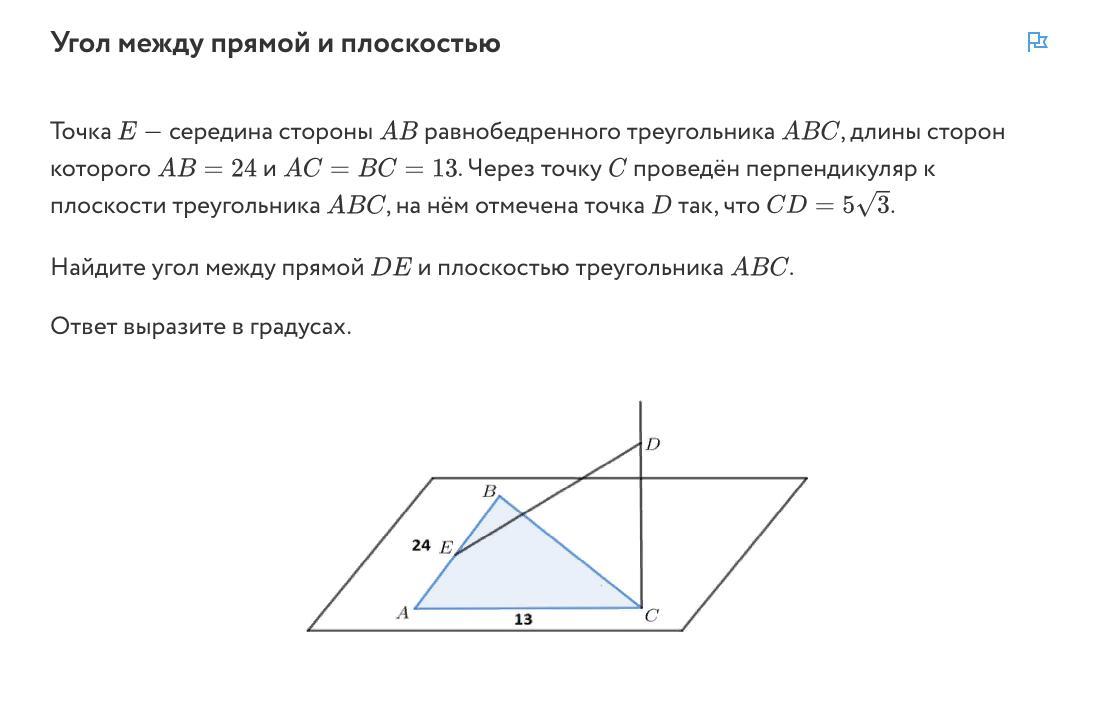
Точка Е середина стороны АВ равнобедренного треугольника АВС, длины сторон которого АВ=24 и АС=ВС=13
Через точку С проведён перпендикуляр к плоскости треугольника АВС, на нём отмечена точка D так, что CD=  .
.
Найдите угол между прямой DE и плоскостью треугольника ABC .
Ответ выразите в градусах.
Приложения:
Ответы
Ответ дал:
8
Ответ:
Объяснение:
ЕС - высота равнобедренного треугольника;
АЕ=АВ/2=24/2-12;
по т. Пифагора ЕС=√(АС²-АЕ²)=√25=5;
треугольник ЕСD прямоугольный по условию;
по т. Пифагора ЕD=√(ЕС²+DЕ²)=10;
ЕD=2ЕС ⇒ ∡EDC=30° и ∡DEC (угол между прямой ЕD и плоскостью АВС) равен 90-30=60°.
esonia4002:
Спасибо!
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад