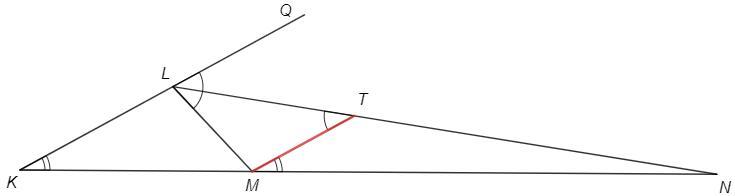
В треугольнике KLM стороны относятся как KL: LM:KM = 12: 8: 16. Биссектриса внешнего
угла L пересекает прямую KM в точке N. Найдите периметр треугольника KLM, если NM = 8.

Ответы

Ответ дал: siestarjoki

Проведем MT||KL

MTL =QLT (накрест лежащие) =MLT => △LMT - равнобедренный, TM=LM

K=TMN (соответственные)

△LKN~△TMN (по двум углам)

LK/TM =KN/MN

LK=12x, LM=8x, KM=16x

12x/8x =(16x+8)/8 => x=1/4

P =(12+8+16)x =36/4 =9

Приложения:

siestarjoki: спасибо

Аноним: cgfcb,j? dfv

Аноним: спасибо, Вам

Аноним: можете помочь пожалуйста с еще одной

Аноним: https://znanija.com/task/39973775

Аноним: идеи в мою тупую бошку не лезут

Аноним: https://znanija.com/task/39995098 ой это

Аноним: Длины основании LM и KN трапеции KLMN равны соответственно 6 и 21.Биссектриса угла
LKN делит сторону MN в отношении 2: 7 считая с вершины M, а биссектриса угла KNM делит
сторону KL в отношении 1: 7 считая с вершины L. Найдите площадь трапеции.

siestarjoki: позже вечером все решу

Аноним: спасибо Вам большое. только вот эту и все.

Вас заинтересует

Другие предметы

2 года назад

Профессия вожатого -это ...

Обществознание

2 года назад

Эссе по обществознанию На тему: некоторые называют глобализацию не Всемирным братством ,а Всемирным пиратством Быстрее пожалуйста!! .

Русский язык

2 года назад

Как много красок в осеннем лесу. Найти главные члены предложения.