Ответы
Ответ дал:
0
Ответ:
Пусть O - точка пересечения AC и BD.
Тогда ∠AOB≡∠COD (как вертикальные углы) и OB≡OD, OA≡OC (по условию).
Следовательно ΔAOB≡ΔCOD по двум равным сторонам и углу между ними.
Это также значит, что ABCD - параллелограмм, и тогда диагональ делит его на равны треугольники (ABC и ACD)
Объяснение:
Ответ дал:
0
Дано - O- точка пересечения
Доказать Δabc=Δcda
Доказательство
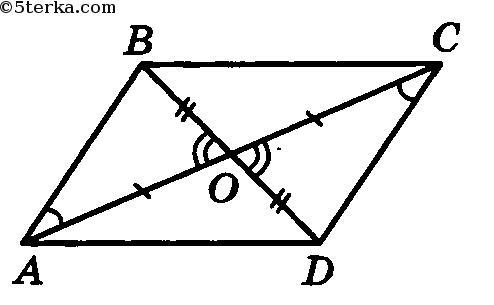
Пусть отрезки ac и bd пересекаются в точке O.
Δaob=Δcod - по 1 признаку ,∠aob, ∠cod - вертикальные
⇒ ΔAOB≡ΔCOD по двум равным сторонам и углу между ними.
1 - ac - общая
2 - ∠bac = ∠acd по 1 признаку (это все в фигурной скобке)
3 ab=cd
⇒ ABCD - параллелограмм, а диагональ делит его на равны треугольники (ABC и ACD)
ч. т. д.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад