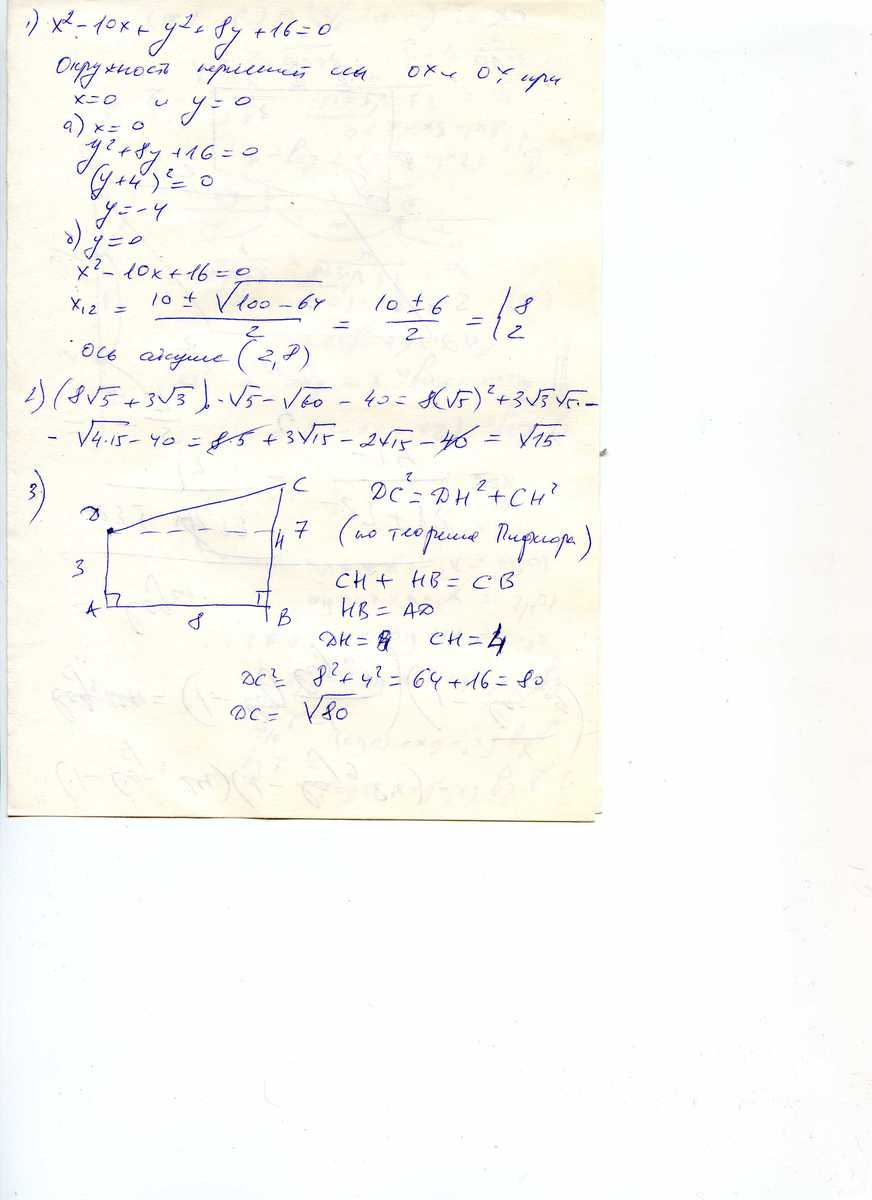
1) окружность задана уравнением х²-10 х +у²+8 у+16=0. Найдите координаты точек пересечения окружности с осью абсцисс .
2) упростите выражение (8√5+3√3)
*√5-√60-40.
3) в приведенном четырехугольнике АДСВ : ДА перпендикулярно АВ , СВ перпендикулярно АВ , АД=3см, АВ=8 см и ВС=7 см. Найдите ДС.
Ответы
Ответ дал:
0
оп оси абсцисс (2;8) по оси ординат (0;-4)
3. Так как они перпендикулярные друг другу, то DC будет равна
Ответ дал:
0
посмотрите ответ в приложении
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
11 лет назад