Question

может ли прямоугольный треугольник иметь стороны равные: 1) 11 см, 7 см, 17 см; 2) 3 см, 1,6 см, 3,4 см; 3) 3 см, 4 см, 6 см; 4) 2 см, √7 см, √11 см? в каждом случае обоснуйте ответ.​

Answer 1

Объяснение:

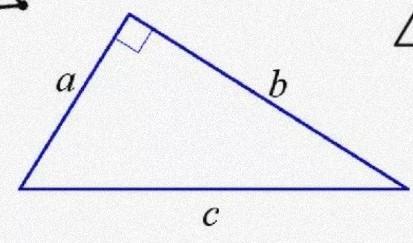
Чтобы проверить это, воспользуемся обратной теоремой Пифагора (проверим, является ли ∆ прямоугольным или нет)

${c}^{2} = {a}^{2} + {b}^{2}$

где a и b - катеты прямоугольного ∆

c - гипотенуза прямоугольного ∆

$1) \: \: {17}^{2} \lor{11}^{2} + {7}^{2} \\ 289 \lor 121 + 49 \\ 289 \ \lor170 = \\ 289 \ne 170$

Значит данный вид ∆ - не прямоугольноый

$2) \: \: {3.4}^{2} \lor{3}^{2} + {1.6}^{2} \\ 11.56 \lor9 + 2.56 \\ 11.56 \lor11.56 \\ 11.56 = 11.56$

Значит этот ∆ - прямоугольный

$3 )\: \: {6}^{2} \lor {3}^{2} + {4}^{2} \\ 36 \lor9 + 16 \\ 36 \lor25 \\ 36 \ne25$

Значит данный ∆ - не прямоугольный

$4) \: \: { (\sqrt{11}) }^{2} \lor {2}^{2} + ( { \sqrt{7}) }^{2} \\ 11 \lor4 + 7 \\ 11 \lor11 \\ 11 = 11$

Значит этот прямоугольник - прямоугольный