Тема: иррациональные уравнения
Приложения:
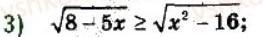
Universalka:
Это не уравнение, а неравенство.
извиняюсь....
Ответы
Ответ дал:
0
///////////////////////////// ///////////////
______[-8]_____[-4]_____[3]_____[4]______
////////////////////////////
Ответ : x ∈ [-8; - 4]
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад