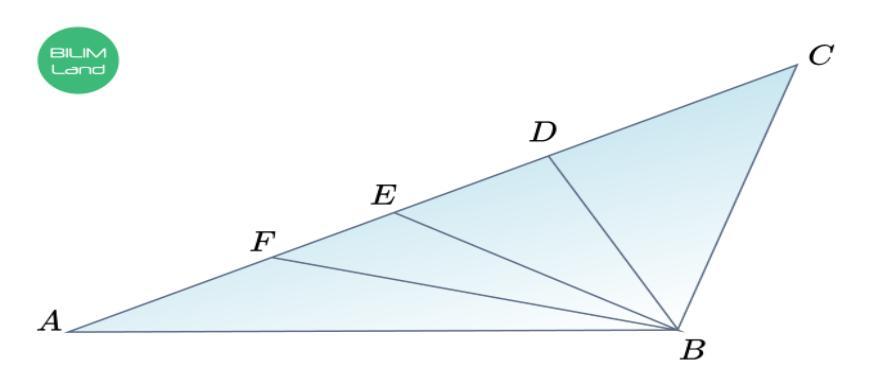
На рисунке BD – биссектриса треугольника ABC, BE – биссектриса треугольника ABD, BF – биссектриса треугольника ABE. Если ∠ABC = 116°, найди следующие углы.
∠FBE =
∠FBC =
∠EBC =
∠FBD =
Приложения:
animeken:
это правильно!
ты д е б и л
ПРАВИЛЬНО СПАСИБО
У КОГО ЛИМИТ
FBE= 14'30
FBC=101'30
EBC=87'
FBD=43'30
Смотрите не перепутайте (е) и (ф) удачи!
а ты молодец
Ответы
Ответ дал:
3
Объяснение:
Дано:
BD – биссектриса треугольника ABC;
BE – биссектриса треугольника ABD;
BF – биссектриса треугольника ABE;
∠ABC = 116°
Найти: ∠FBE, ∠FBC, ∠EBC, ∠FBD.
Решение:
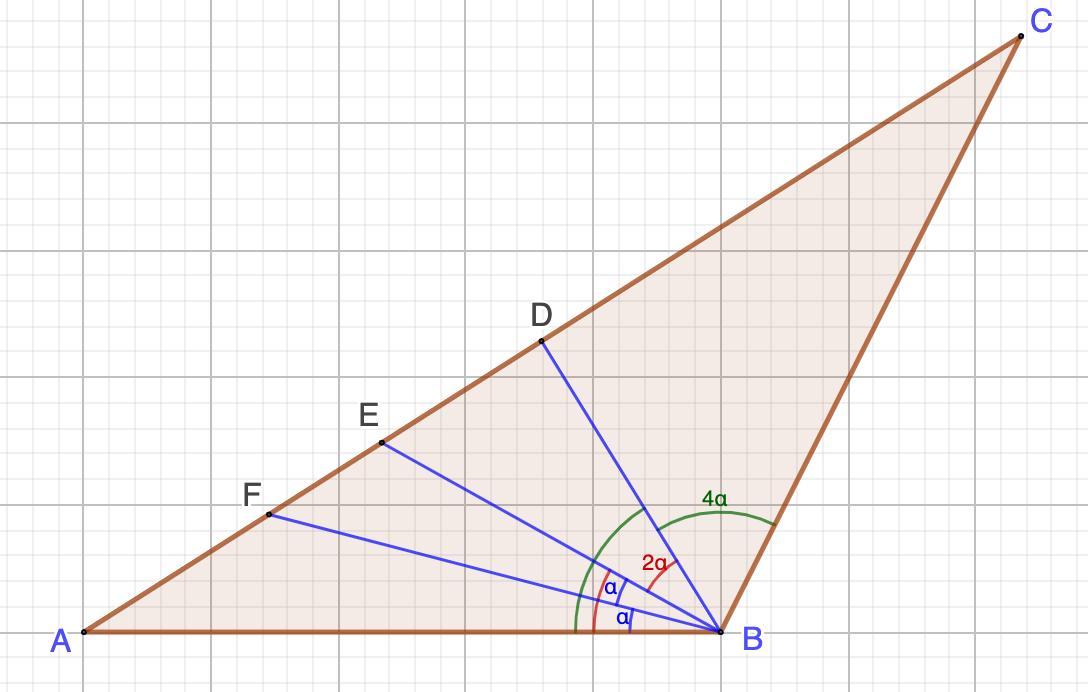
См. рис.
Пусть ∠ABF=∠FBE=α (BF – биссектриса ∠ABE),
тогда ∠ABE=∠EBD=2α (BE – биссектриса ∠ABD),
a ∠ABD=∠DBC=4α (BD – биссектриса ∠ABC).
⇒ ∠ABC=8α=116°
Найдем α:
α=116°:8=14,5°
Теперь найдем искомые углы:
- Если угол разделен на части, то градусная мера всего угла равна сумме градусных мер его частей.
∠FBE=α=14,5°
∠FBC=∠FBE+∠EBD+∠DBC=α+2α+4α=7α=14,5°·7=101,5°
∠EBC=∠EBD+∠DBC=2α+4α=6α=14,5°·6=87°
∠FBD=∠FBE+∠EBD=α+2α=3α=14,5°·3=43,5°
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад