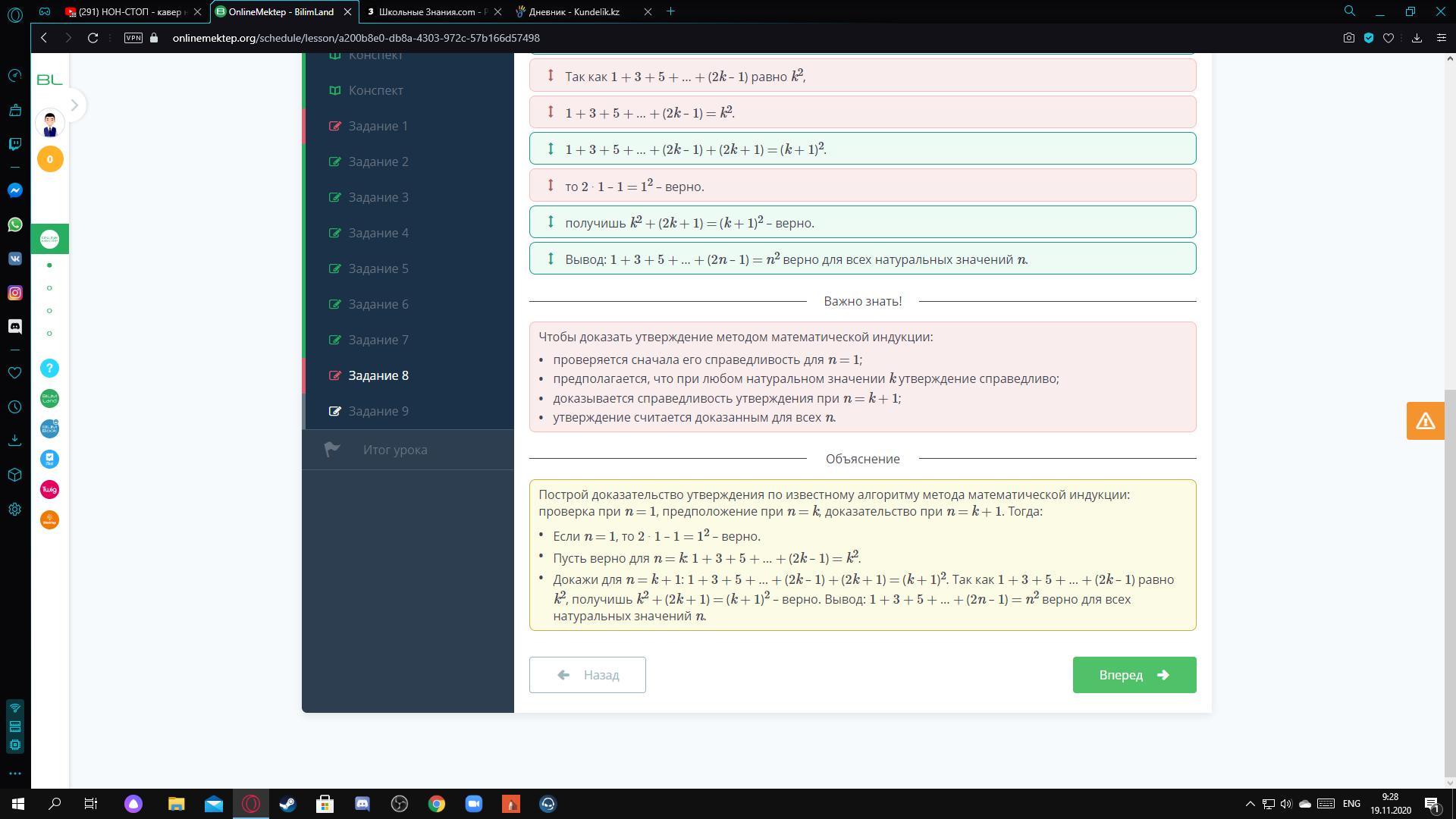
Дано утверждение: «Для всех натуральных n выполняется равенство 1 + 3 + 5 + … + 2(n – 1) = n2». Отсортируй беспорядочные этапы доказательств данного утверждения (сверху вниз).
Приложения:

3 4 5 неправельный
Сами исправите
Ок?
Ответы
Ответ дал:
35
Объяснение: ответ на фото смотри
Приложения:
спсибо
что с качеством непонятно ниче
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
то 2 ∙ 1 – 1 = 12 – верно.
Докажи для n = k + 1:
Пусть верно для n = k:
1 + 3 + 5 + ... + (2k – 1) = k2.
1 + 3 + 5 + ... + (2k – 1) + (2k + 1) = (k + 1)2.
Так как 1 + 3 + 5 + ... + (2k – 1) равно k2,
получишь k2 + (2k + 1) = (k + 1)2 – верно.
Вывод: 1 + 3 + 5 + ... + (2n – 1) = n2 верно для всех натуральных значений n.