Question

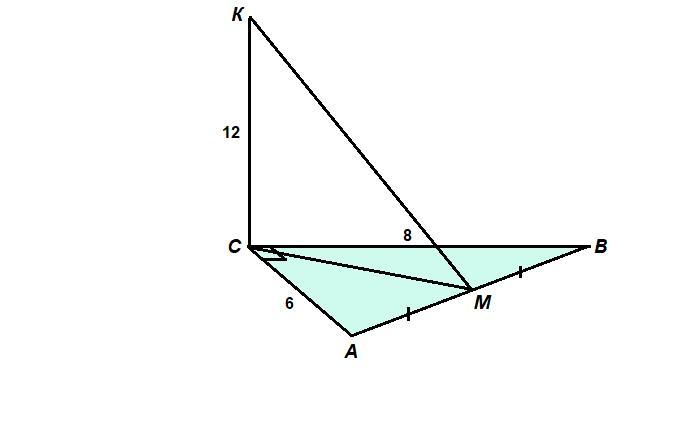
У трикутнику АВС ∠С = 90°, АС = 6 см, ВС = 8 см, СМ — медіана. Через вершину С проведено пряму CK, яка перпендикулярна до площини трикутника АВС, причому CK = 12 см. Знайдіть KM.

Answer 1

Ответ:

13 см

Объяснение:

По теореме Пифагора найдем гипотенузу:

AB = √(AC² + BC²) = √(6² + 8²) = √(36 + 64) = √100 = 10 см

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине.

СM = 1/2 АВ = 1/2 · 10 = 5 см

СК ⊥ (АВС), СМ лежит в плоскости (АВС), значит СК ⊥ СМ.

Из прямоугольного треугольника СКМ по теореме Пифагора:

KM = √(CK² + CM²) = √(12² + 5²) = √(144 + 25) = √169 = 13 см