Question

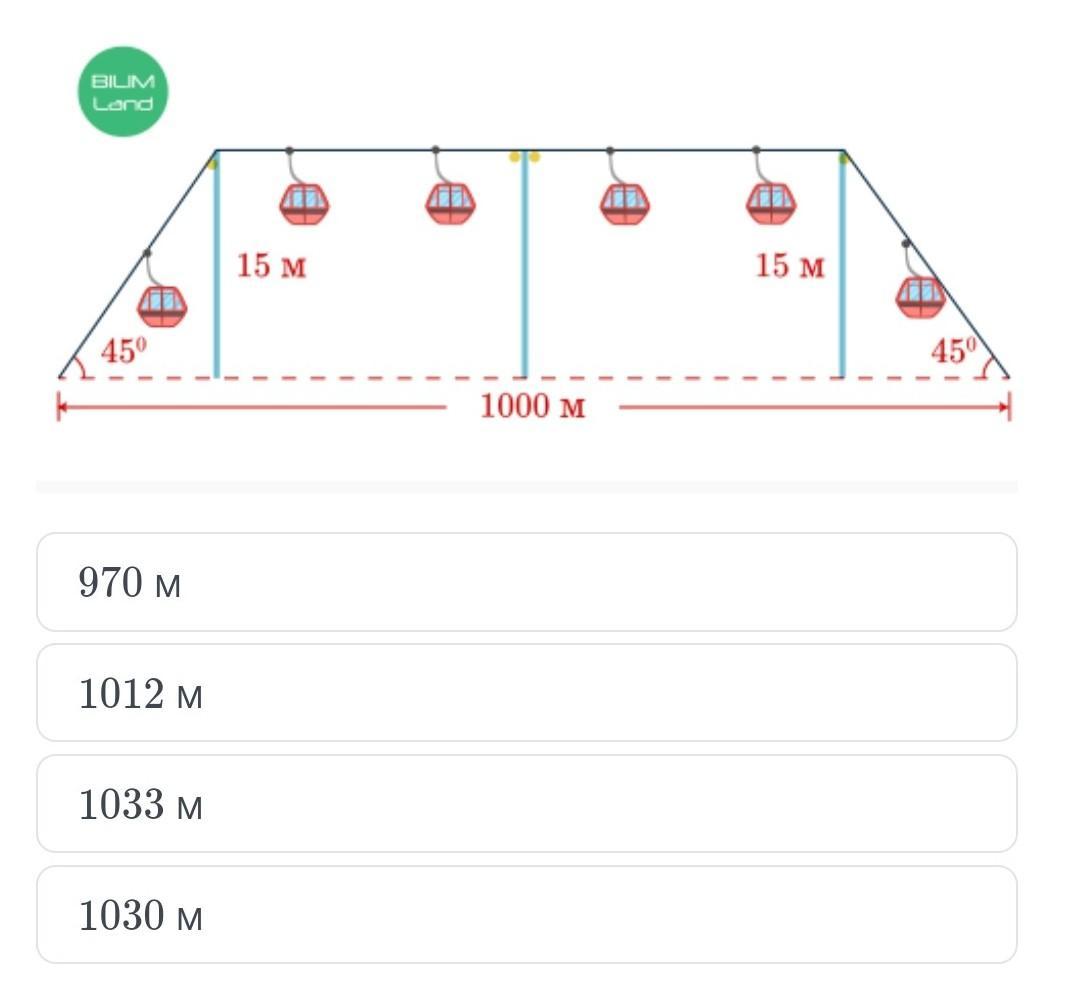
На схеме показан аттракцион, в котором трамвайные вагоны скользят по канату. Какова длина каната? Ответ округли до целых.​

Answer 1

Ответ:

1012 м

Объяснение:

Аттракцион представляет собой равнобедренную трапецию (углы при основании равны), в которой нижнее основание равно 1000 м, высота равна 15 м.

Надо найти сумму боковых сторон и верхнего основания трапеции.

Обозначим трапецию ABCD, высоты - ВН и СК.

Рассмотрим ΔАВН:

  ∠АНВ = 90°, ∠ВАН = 45°, значит

  ∠АВН = 90° - ∠ВАН = 90° - 45° = 45° (сумма острых углов прямоугольного треугольника равна 90°).

  ∠АВН = ∠ВАН = 45°  ⇒  АН = ВН = 15 м

  По теореме Пифагора:

  $AB=\sqrt{AH^2+BH^2}=\sqrt{15^2+15^2}=\sqrt{15^2\cdot 2}=15\sqrt{2}$  м

CD = AB = 15√2 м

ΔАВН = ΔDCK по гипотенузе и катету (АВ = СD, так как трапеция равнобедренная, ВН = СК как высоты трапеции), значит

DK = АН = 15 м

НК = AD - (AH + KD) = 1000 - (15 + 15) = 970 м

ВНКС - прямоугольник, так у него все углы прямые.

ВС = НК = 970 м

Длина каната:

AB + BC + CD = 15√2 + 970 + 15√2 = 970 + 30√2 м

970 + 30√2 ≈ 970 + 30 · 1,4 ≈ 970 + 42 ≈ 1012 м