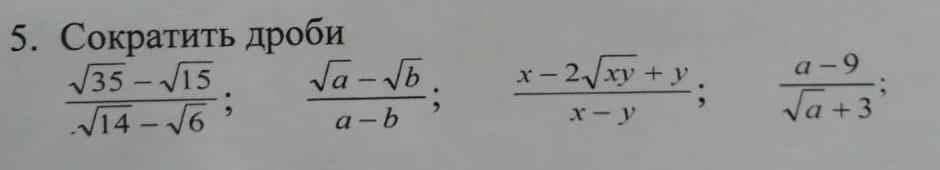Ответы
Ответ дал:
1
Ответ дал:
1
Ответ:
1)
2)
3)
4)
Объяснение:
#1
- Избавимся от иррациональности в знаменателе
- Перемножим выражения в скобках
#2
Формула разности квадратов:
- Воспользуемся ею
#3
Формула квадрата разности:
- Воспользуемся ею и формулой квадрата разности (описывал #2)
#4
- Воспользуемся формулой квадрата разности (описывал #2)
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад