Ответы
Ответ:
(- а/b ; - а³/b ) -координаты точки пересечения.
(0;0) -координаты другой точки пересечения
(а/b ; а³/b ) -координаты третьей точки пересечения
Объяснение:
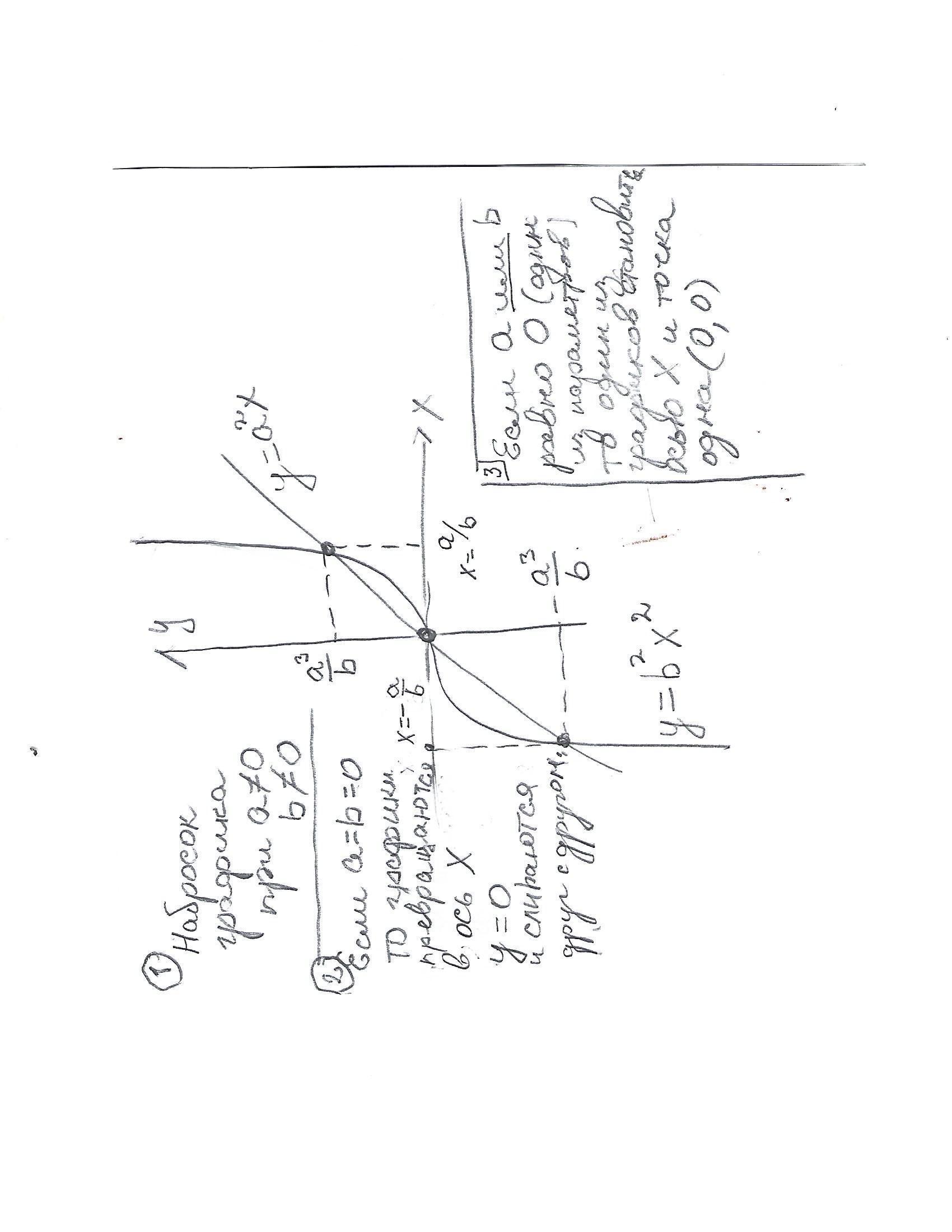
При а≠0 и b≠0
y=a²x и y=b²x³ Найдем точки равенства функций
0=b²x³-a²x
0=(b²x²-a²)x
произведение равно 0 при равенстве 0 одного из сомножителей.
х₁ =0
или b²x²-a²=0
b²x²=a²
х²=а²/b² для х , а и b возможны как положительные,так и отрицательные значения х∈{ - а/b ; а/b}
из всех вариантов а/b = -а/-b и - а/b = а/-b совпали.
х₄ =а/b = х₅ = -а/-b = а/b
х₂= - а/b = х₃ =а/-b= - а/b
Поэтому осталось только три значения Х.
х₁ =0; х₂= - а/b ; х₃ =а/b три точки пересечения графиков.
Это на оси абсцисс.
Найдем соответствующие им значение ординат
y=a²x и y=b²x³
а) х=0 y=a²*0=0 (0;0) х=0 y=b²*0=0 (0;0)
(0;0) - координаты точки пересечения графиков
б) х₂= - а/b х₂= - а/b
y=a²*( - а/b ) = - а³/b y=b²(-а/b)³=-а³b²/b³=- а³/b
(- а/b ; - а³/b ) - координаты точки пересечения графиков.
в) х =а/b х =а/b
y=a²*( а/b ) = а³/b y=b²(а/b)³=а³b²/b³= а³/b
( а/b ; а³/b ) -координаты точки пересечения графиков.
1) Для случая когда а и b не равны 0 есть три точки пересечения.
2) когда и а,и b равны 0. Функции превращаются в у=0 и сливаются друг с другом.Все точки общие.
3) Если один из параметров а или b 0,а другой нет,получается пересечение оси Х с одной из функций (параметр которой не равен 0) и всего одна точка пересечения (0;0)