СРОЧНО ПОМОГИТЕ
докажите что биссектрисы равнобедренного треугольника проведенные из вершин острых углов при основании равны
Ответы
Ответ дал:
2
Ответ:
Дано:
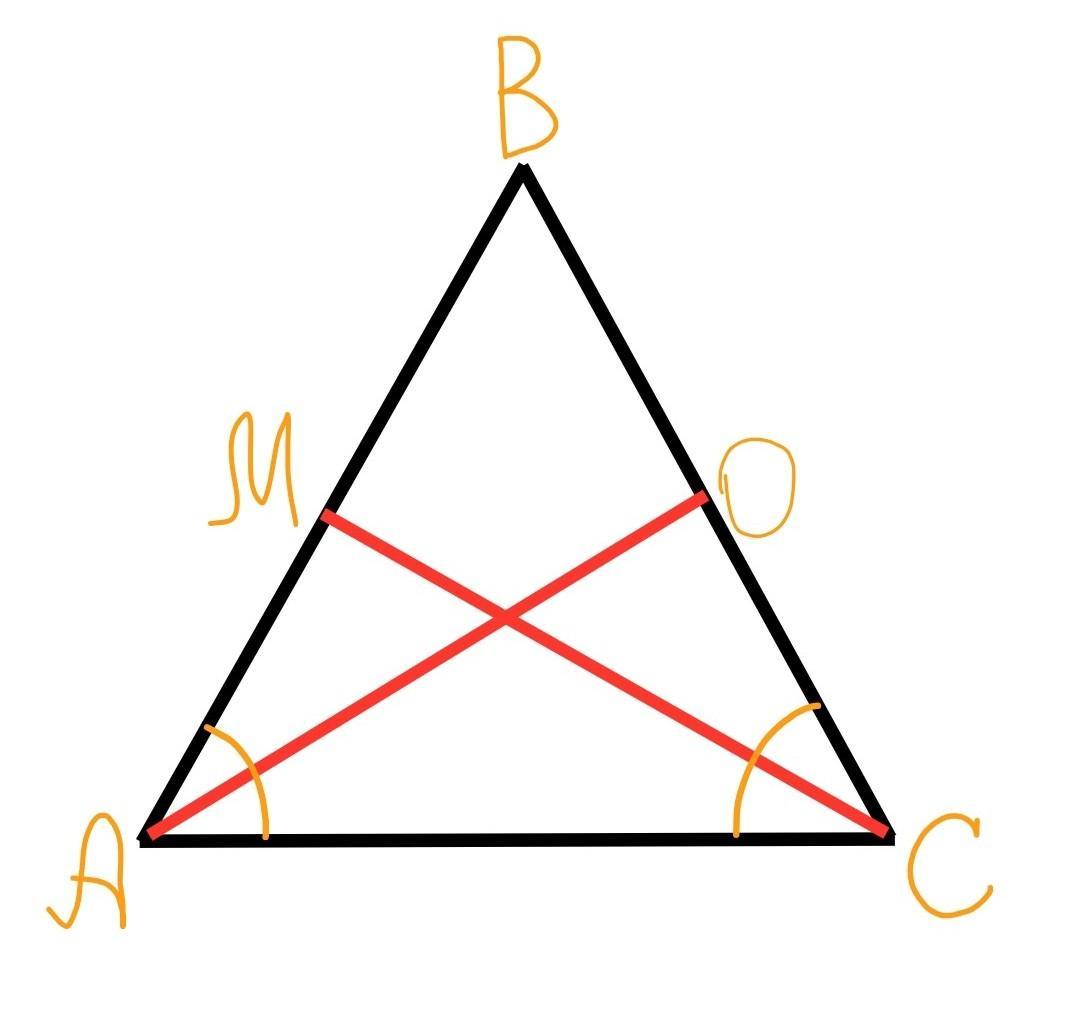
∆АВС – равнобедренный с основанием АС;
АО и СМ – биссектрисы углов ВАС и ВСА соответственно.
Доказать: АО=СМ
Решение:
Рассмотрим ∆АОС и ∆СМА.
АС – общая сторона;
Угол АСО=угол САМ, так как углы при основании равнобедренного треугольника равны. Следовательно 0,5*угол АСО=0,5*угол САМ.
Так как АО и СМ – биссектрисы по условию, то угол САО=0,5*САМ; угол АСМ=0,5*угол АСО.
Тогда угол САО=угол АСМ.
Следовательно из всех найденных равенств:
∆АОМ=∆СМА по двум углам и стороне между ними.
Следовательно АО=СМ как соответственные стороны равных треугольников.
Доказано.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад