Ответы
Ответ дал:
1
Ответ:
14 см ².
Объяснение:
Площадь параллелограмма определяется по формуле :
где
- угол между сторонами а и b.
Тогда найдем площадь параллелограмма
Тогда площадь параллелограмма равна 14 см ².
Приложения:
Ответ дал:
2
Ответ:
14 см²
Объяснение:
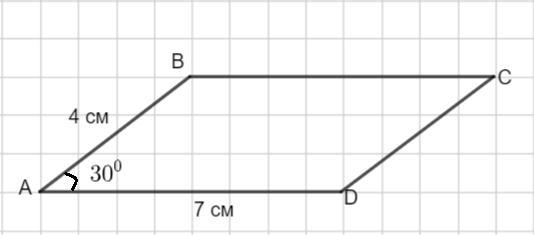
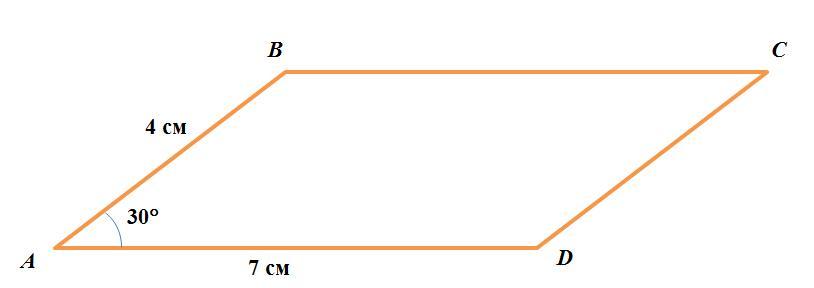
Дано (см. рисунок):
AB = 4 см
AD = 7 см
∠BAD = 30°
Найти: S(ABCD) - площадь.
Решение. Площадь параллелограмма S через стороны a и b и угол α между ними определяется по формуле:
S = a · b · sinα.
Подставляем известные значения и находим площадь параллелограмма:
S(ABCD) = 4 · 7 · sin30° = 28 · 0,5 = 14 см².
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад