Помогите пожалуйста.
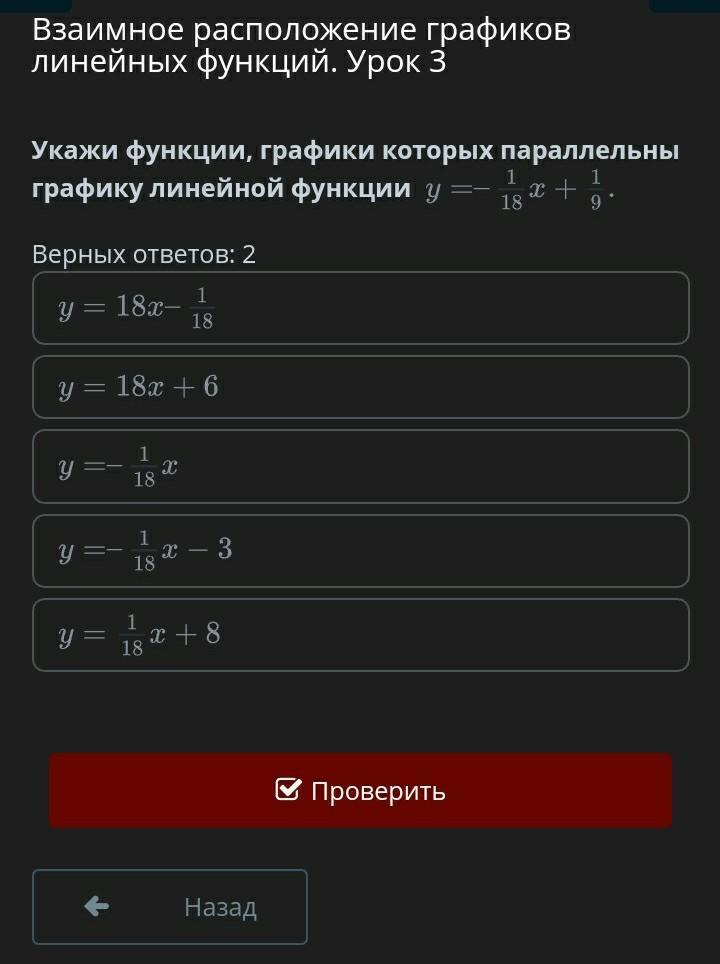
Укажи функции, графики которых параллельны графику линейной функции
Верных ответов: 2
Приложения:
Аноним:
верный ответ y= -1/18x и у=-1/18x-3 пожалуйста :)
Спачибо♂️
Ответы
Ответ дал:
1
Ответ:
Объяснение:
Нужно знать:
Графики линейных функций y=k₁·x+b и y=k₂·x+d будут параллельными, если угловые коэффициенты равны, то есть k₁=k₂.
Решение. Дана функция
с угловым коэффициентом .
Сравним угловые коэффициенты функций и определим, что только функции (см. рисунок)
и
имею угловой коэффициент .
Значит, только графики этих функций параллельны графику заданной функции.
Приложения:

Вас заинтересует
2 года назад
2 года назад
9 лет назад