Question

В ∆ABC ∠C = 90°, CD – высота, tg ∠DCB =3/4. Найди отношение высоты CD к катету AC.

Answer 1

Ответ:

$\boxed{\cfrac{CD}{AC} = \frac{3}{5} = 0,6 }$

Объяснение:

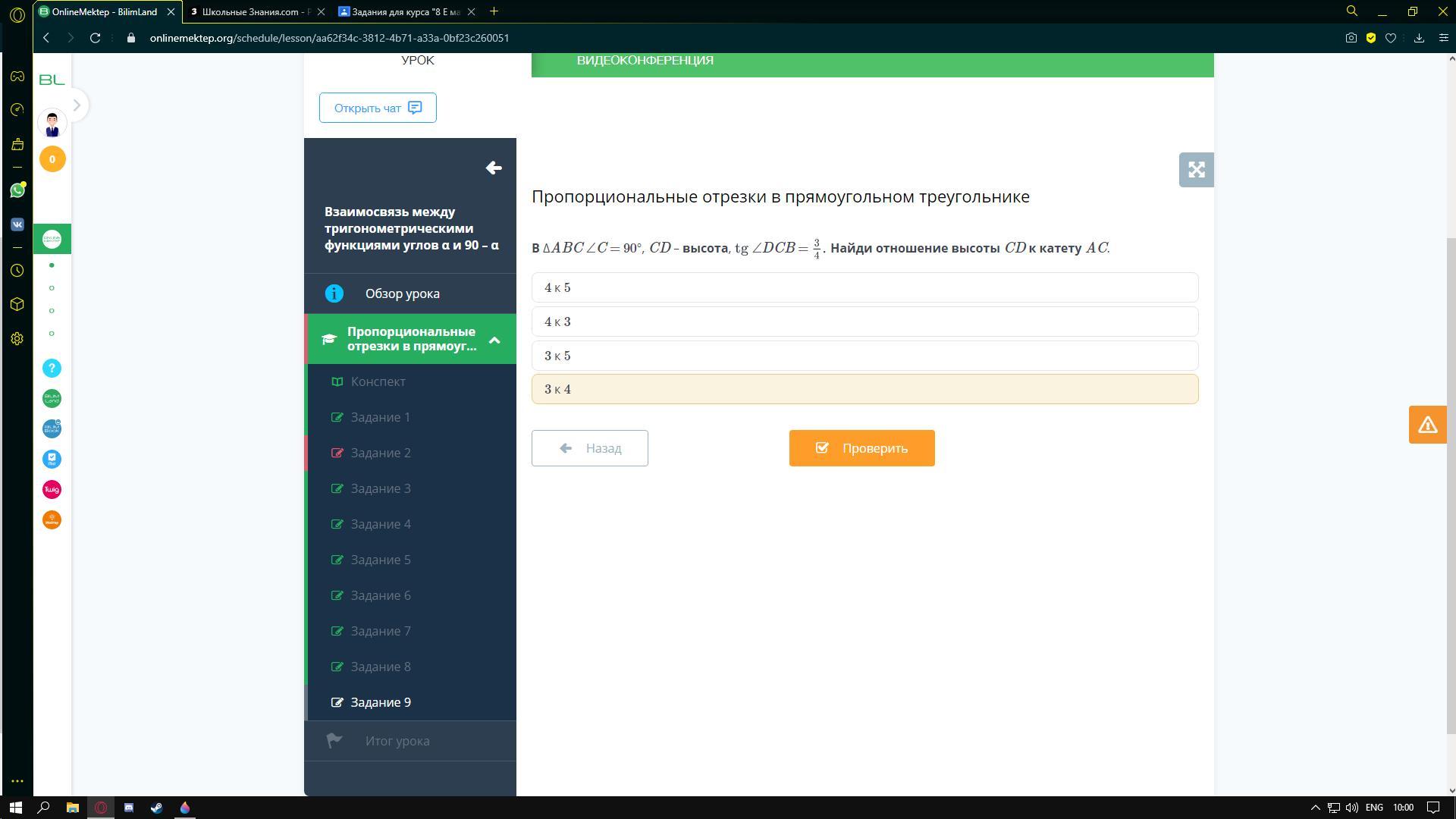
Дано: ∠C = 90°, CD – высота, tg ∠DCB = 3/4

Найти: $\dfrac{CD}{AC}$ - ?

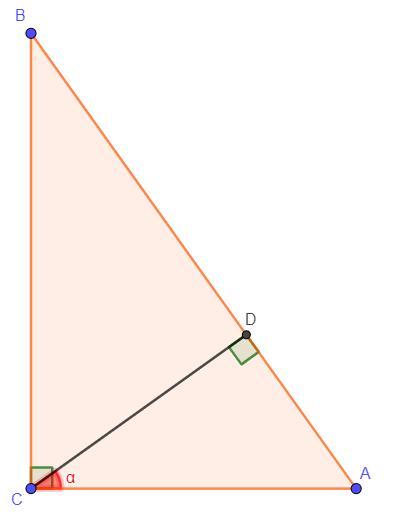
Решение: Рассмотрим треугольник ΔCDA. Так как CD – высота по условию, то угол ∠CDA = 90°, следовательно треугольник ΔCDA - прямоугольный. Так как угол ∠DCA - угол прямоугольного  треугольника ΔCDA и ∠DCA ≠ 90°, то тригонометрические функции от угла ∠DCA будут больше нуля. Пусть угол ∠DCA = α.

Угол ∠С = ∠DCA + ∠DCB ⇒ ∠DCB = ∠C - ∠DCA = 90° - α

tg (∠DCB) = tg(90° - α)

tg ∠DCB = ctg α ⇒ tg α = $\dfrac{1}{tg \ \angle DCB} = \dfrac{\dfrac{1}{1} }{\dfrac{3}{4} } = \dfrac{4}{3}$

По основному тригонометрическому тождеству:

$\sin^{2} \alpha + \cos^{2} \alpha = 1$

$\sin^{2} \alpha + \cos^{2} \alpha = 1|: \cos^{2} \alpha$

$tg^{2} \alpha + 1 = \dfrac{1}{\cos^{2} \alpha }$

$\cos^{2} \alpha = \dfrac{1}{tg^{2} \alpha + 1}$

$\cos \alpha = \sqrt{ \dfrac{1}{tg^{2} \alpha + 1}} = \sqrt{\dfrac{1}{\dfrac{16}{9} + 1} } = \sqrt{\dfrac{1}{\dfrac{16}{9} + \dfrac{9}{9} } } = \sqrt{ \dfrac{1}{\dfrac{25}{9} } } = \sqrt{\dfrac{9}{25} } = \dfrac{3}{5} = 0,6$

По определению косинуса в прямоугольном треугольнике(ΔCDA):

$\cfrac{CD}{AC} = \cos \alpha = 0,6$