Question

дан параллелограмм, биссектриса тупого угла делит противолежащие стороны 3:7, считая от вершины острого угла. Периметр параллелограмма равен 117. Найти: большую сторону параллелограмма.

Answer 1

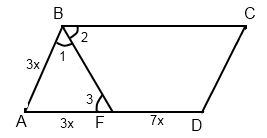
Дано: ABCD - параллелограмм,
BF - биссектриса,
AF:FD=3:7
P=117 см
Найти: большую сторону параллелограмма.
Решение.
AF:FD=3:7
Пусть x - коэффициент пропорциональности.
ТОгда AF=3х, FD=7х
Значит,  AD=BC=10х

<1=<2 - т.к. BF - биссектриса
<2=<3 - как внутренние накрест лежащие углы при  AD параллельно BC и секкущей  BF.
Значит,  <1=<3 и треугольник ABF - равнобедренный, AF=AB=3х.

Периметр параллелограмма P=10x+10x+3x+3x=26x=117
x=117/26=4$frac{13}{26}$=4,5

ТОгда AD=10х=10*4,5=45

Ответ: 45 см