В окружности проведена хорда, равная радиусу. Чему равна величина вписанного угла, опирающегося на эту хорду?
Ответы
Ответ дал:
1
Ответ:
∠ACB = 30°
Объяснение:
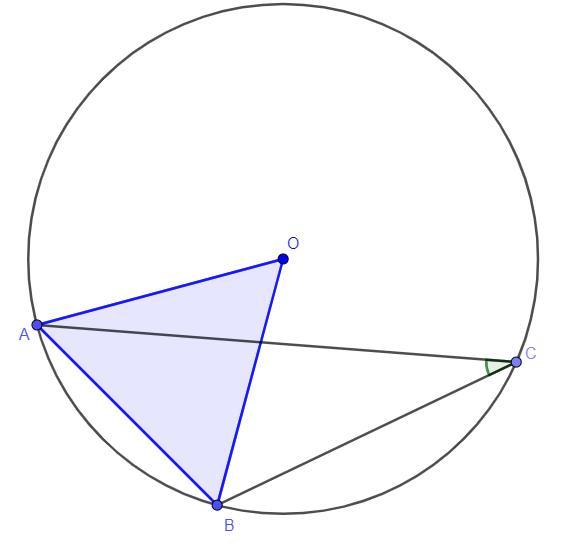
Дано: O - центр окружности, OA = OB = AB (OA = OB как радиусы)
Найти: ∠ACB - ?
Решение: Так как по условию OA = OB = AB, то треугольник ΔAOB - правильный, следовательно по свойствам правильного треугольника все его углы равны 60°, тогда ∠AOB = 60°. Градусная мера дуги равна градусной мере центрального угла, который опирается на эту дугу, тогда ∪AB = ∠AOB = 60°. По теореме градусная мера вписанного угла равна половине дуги, на которую он опирается, тогда
∠ACB = 0,5∪AB = 0,5 * 60° = 30°.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад