Question

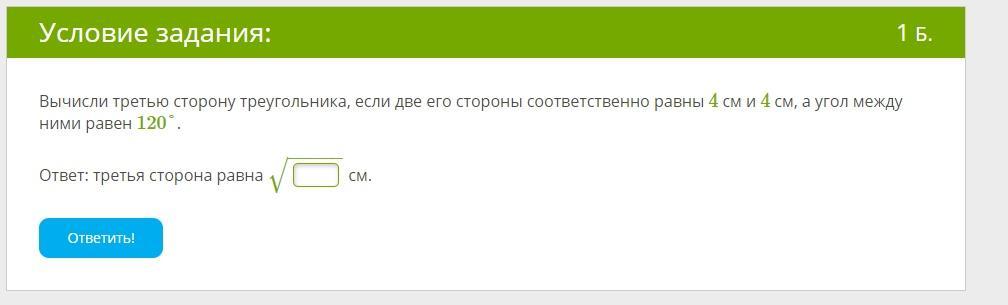
Вычисли третью сторону треугольника, если две его стороны соответственно равны 4 см и 4 см, а угол между ними равен 120°.

Ответ: третья сторона равна
−−−−−√ см.

Answer 1

Ответ:

Объяснение:

Теорема косинусов:

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

а²=b²+c²-2*b*c*cosA.

______________________

Дано:

∆АВС

АВ=АС=4 см

∡А=120°

_________

ВС=?

По т. косинусов:

ВС²=АВ²+АС²-2*АВ*АС*соsA

ВС²=4²+4²-2*4*4*соs120°

ВС²=16+16-8*4*соs(180°-60°)

ВС²=32-32*(-соs60°)

ВС²=32-32*(-1/2)

ВС²=32-(-16)

ВС²=32+16=48⇒

ВС=√48 см.

Примечание: √48 можно упростить:

√48=√(16*3)=√(4²*3)=4√3 см.