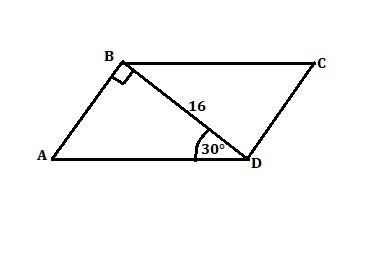
Диагональ BD параллелограмма ABCD перпендикулярна стороне AB и равна 16 см. вычислите длины сторон параллелограмма, если угол BDA равен 30°.
можно пожалуйста с чертежом и дано, заранее благодарю
Ответы
Ответ дал:
41
Ответ:
АВ = CD = 3,2·√5 см.
AD = BC = 6,4·√5 см.
Объяснение:
Треугольник АВD прямоугольный (∠ABD = 90° (дано).
Против угла 30° лежит катет, равный половине гипотенузы, тогда AD=2·AB.
По теореме Пифагора: АВ² + AD² = BD² или
АВ² + (2·АВ)² = BD² => 5·AB² = 16² =>
АВ = √(16²/5) = 16/√5 = (16√5)/5 = 3,2·√5 см.
AD = 2·АВ = 6,4·√5 см.
Проверка:
BD = √((3,2·√5)²+(6,4·√5)²) = √(51,2+204,6) = √256 = 16.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад