Question

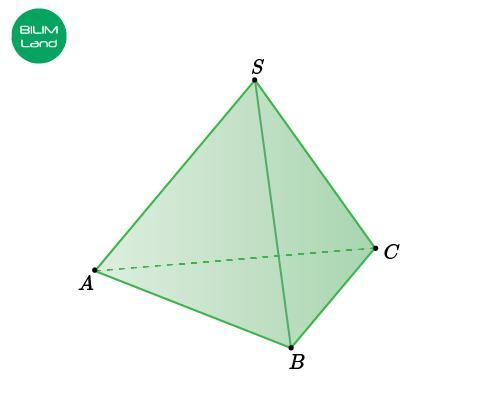
На чертеже дан правильный тетраэдр ABCS, длина ребра которого равна 6. Найди расстояние от точки S до плоскости ABC.

Answer 1

Ответ:

2√6см

Объяснение:

Дано

Тетраэдр

АВ=ВС=АС=SA=SB=SC=6 см

SO=?

Решение.

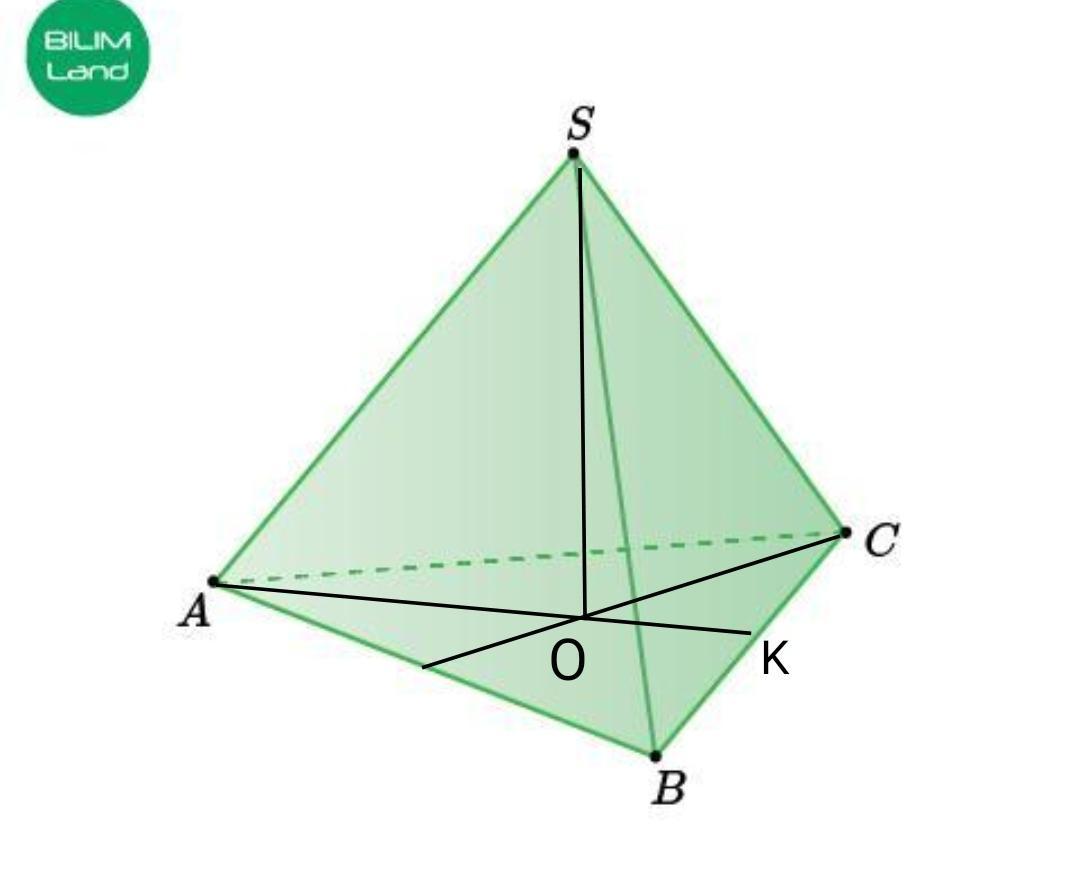
Высота треугольника ∆АВС

АК=АВ√3/2=6√3/2=3√3 см.

т.О пересечение медиан, делит АК в отношении 2:1, начиная от вершины.

АО:ОК=2:1.

АО=АК:3*2=3√3:3*2=2√3 см.

∆АОS - прямоугольный.

SA- гипотенуза.

АО и SO- катеты.

По теореме Пифагора найдем катет

SO²=SA²-AO²=6²-(2√3)²=36-12=24

SO=√24=2√6см