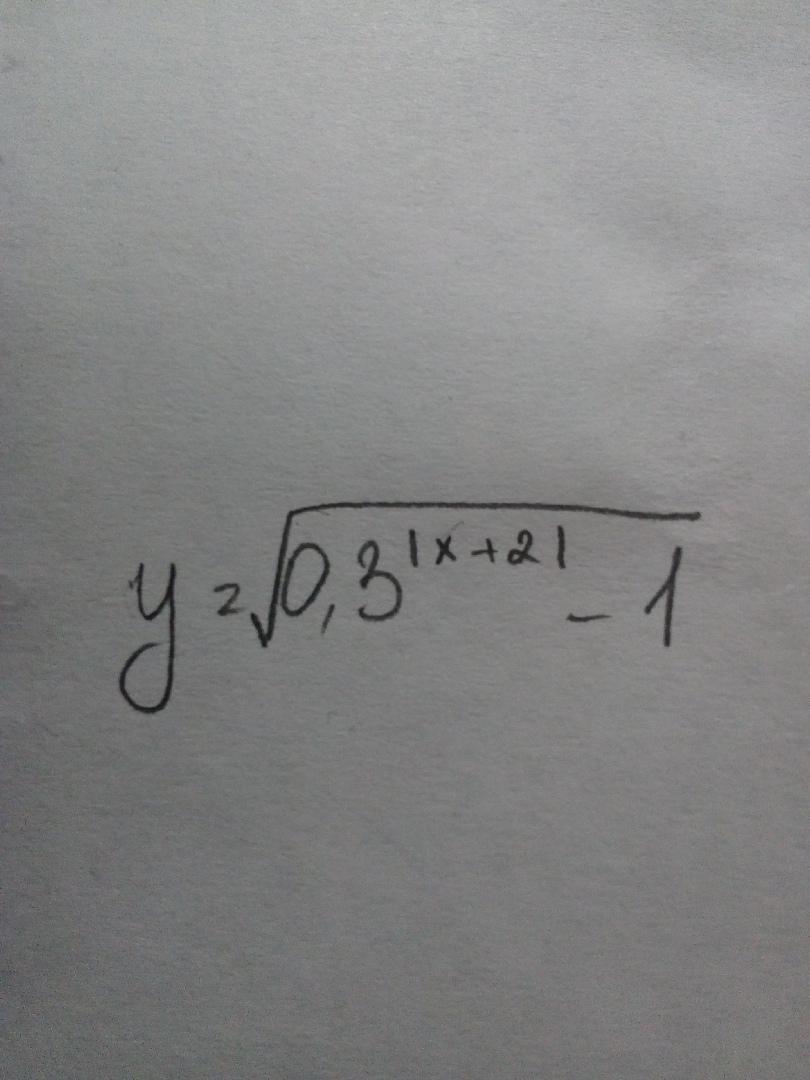Ответы
Ответ дал:
2
Подкоренное выражение корня чётной степени должно быть неотрицательным, то есть ≥ 0.
Ответ дал:
3
Ответ:
Так как модуль положителен ⇒
DocAlfer:
модуль не может быть меньше нуля!!!!
полностью с Вами согласна, ответ неверный
Дописать не дали))
ладно не дали как раз и дописал про x < = -2 а так бы написал, что модуль не отрицательный и x = -2 ))))
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад