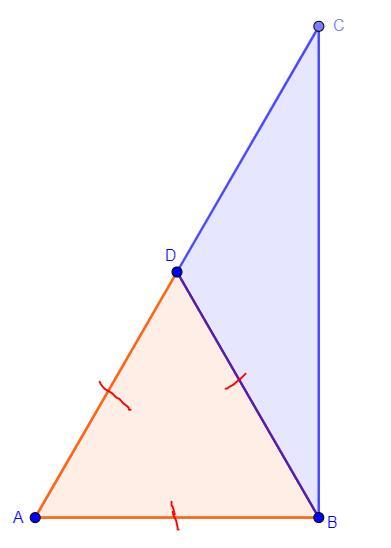
Треугольник ADB равносторонний, сторона DB является медианой треугольника ABC. Угол BCA=30. Определите углы треугольника BDC.
Ответы
Ответ дал:
6
Ответ:
∠BDC = 120°
∠CBD = 30°
Объяснение:
Дано: AD = DB = AB, AD = DC, ∠BCA = 30°
Найти: ∠BDC, ∠CDB - ?
Решение: Так как по условию треугольник ΔADB - равносторонний, то по свойствам равностороннего все его углы 60°, тогда ∠DAB = ∠ABD = =∠BDA = 60°. Угол ∠ADB и ∠СDB - смежные. По свойству смежных углов из сумма 180°. ∠ADB + ∠СDB = 180° ⇒ ∠СDB =
= 180° - ∠ADB = 180° - 60° = 120°. Рассмотрим треугольник ΔCDB. По теореме про сумму углов треугольника: ∠CDB + ∠BCA + ∠CBD = 180° ⇒ ∠CBD = 180° - ∠CDB - ∠BCA= 180° - 120° - 30° = 30°.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад