Question

помогите решить задачу 70 баллов!

Answer 1

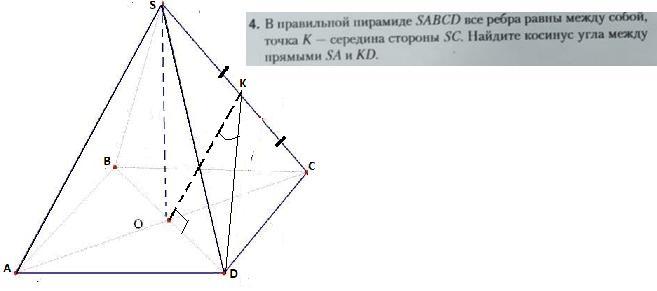
В правильной пирамиде SABCD все ребра равны между собой , точка К-середина SC.Найти косинус угла между прямыми SA и KD

Объяснение:

1) Пирамида правильная, значит в основании квадрат.Пусть каждое ребро пирамиды а.

В ΔASC , отрезок КО-средняя линия , т.к. К-середина по условию, О-середина , как точка пересечения диагоналей квадрата.По т. о средней линии треугольника КО║AS⇒ поэтому углом между  SA и KD  можно считать угол между прямыми ОК и KD или ∠ОКD.

2) SO⊥AC,SO⊥BD⇒ (SAC)⊥(FDC) ⇒OK⊥AC ⇒ΔОКD-прямоугольный ,

cos∠OKD=$\frac{OK}{KD}$  ,

• OK=1/2*AS=1/2*a . по т. о средней линии треугольника;
• Из ΔSKD- прямоугольного( т.к медиана KD , в равностороннем треугольнике является высотой) , по т. Пифагора ,  KD=√(a²-(0,5a)²)=√(0,75a²)=$\frac{a\sqrt{3} }{2}$  .  

cos∠OKD=$\frac{\frac{a}{2} }{\frac{a\sqrt{3} }{2}}=\frac{1}{\sqrt{3} }$   , cos∠OKD=$\frac{\sqrt{3} }{3}$ .