Question

Вычисли углы треугольника AOB, если ∪AnB= 50°, O — центр окружности.

Answer 1

Ответ:

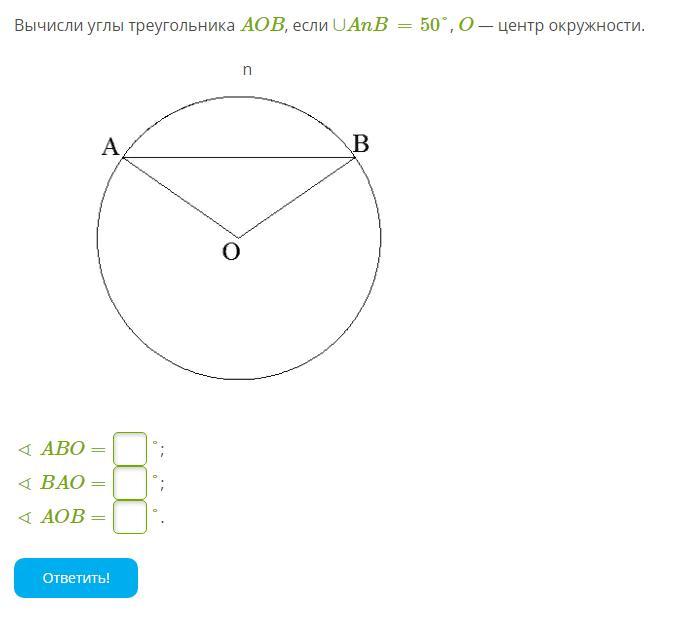
∠АВО = 65°

∠ВАО = 65°

∠АОВ = 50°

Объяснение:

Поскольку дуга ∪AnB= 50°, то соответствующий ей центральный угол

∠АОВ = 50°

АО = ВО - радиусы окружности, поэтому ΔАОВ - равнобедренный, и

∠АВО = ∠ВАО

По свойству углов треугольника

∠АОВ + ∠АВО + ∠ВАО = 180°

или

∠АОВ + 2 · ∠АВО = 180°

и

∠АВО = 0,5 · (180° - ∠АОВ) = 0,5 · (180° - 50°)= 65°

∠ВАО = ∠АВО = 65°

Answer 2

Ответ:∠AOB-центральный угол. Тогда по определению он равен дуге AnB, то есть ∠AOB=50°.

AO=OB как радиусы, отсюда треугольник AOB - равнобедренный.

Тогда, углы при основе ΔAOB равны. Значит ∠ ABO = ∠BAO = (180°- 50°)/2=130°/2=65°

Ответ: ∠ABO = 65°, ∠BAO = 65°, ∠AOB = 50°.

Объяснение: