Ответы
Ответ:
Объяснение:№1
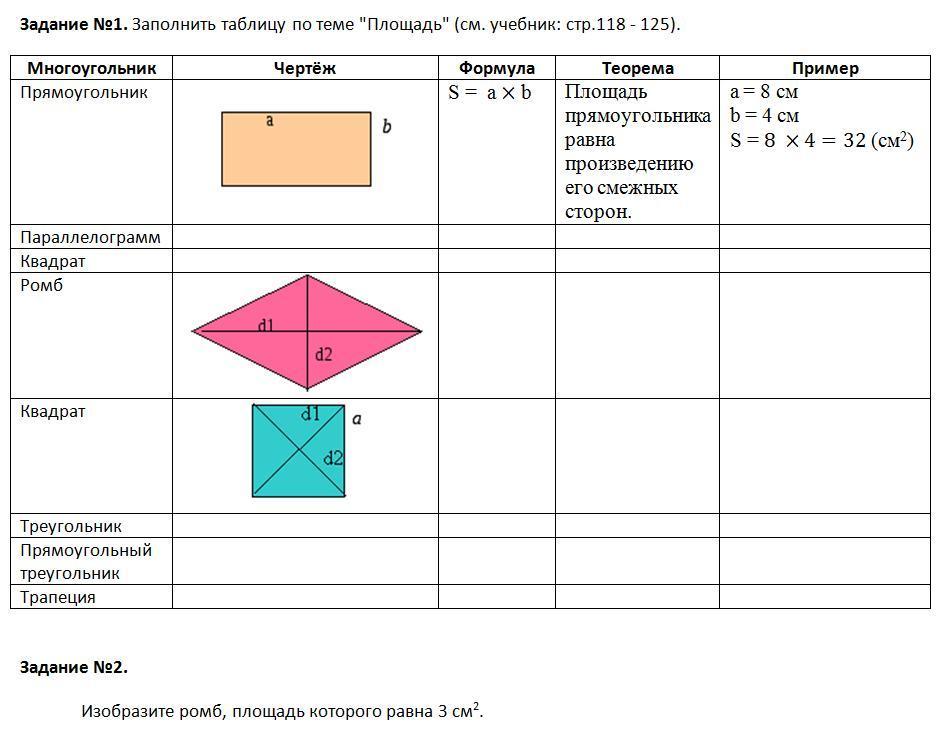
S_{ABCD} = AB·ВС
S_{ABCD}= 6 · 3 = 18
Ответ: 18.
№2
АBCD — прямоугольник. Значит, АВ = CD и BC = AD.
По условию BC = AВ. Значит, АВ = CD = BC = AD.
АВСD по определению квадрат.
P_{ABCD} = 28, значит АВ = CD = BC = AD=7
S_{ABCD} = 7 · 7 = 49
Ответ: 49.
№3.
Рассмотрим ΔАСD. ∠АСD = 60º, ∠АDС = 90º. Можем найти ∠САD = 90º — 60º= 30º.
СD = \frac {AC}{2}
(Катет, лежащий напротив угла 30° равен половине гипотенузы)
CD = 6.
S_{ABCD} = CD · AD.
S_{ABCD} = 6 · 10 = 60.
Ответ: 60.
№4.
Пусть ВС=х, тогда АВ=3х. С другой стороны АВ = 12 + х. Составляем уравнение:
3х = 12 + х;
2х = 12;
х=6.
ВС=6; АВ=3·6=18.
S_{ABCD} = ВС · AВ.
S_{ABCD} = 6 · 18 = 108.
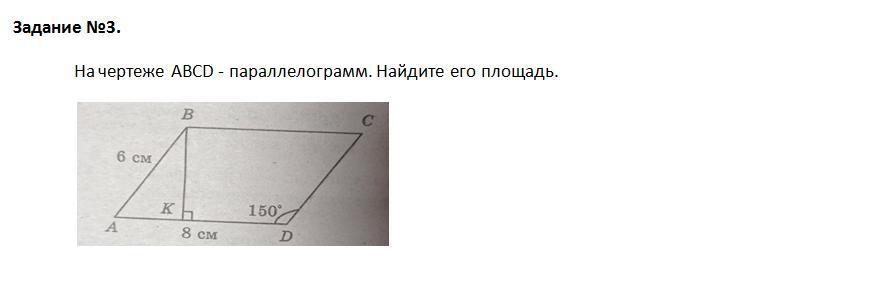
2рисунок ABCD- паралелограмм, следовательно его площадь = высота*основание
1. угол В=150
угол А= 180-угол В(односторонние углы при ВС||АD), угол А=30
2.проведем высоту ВН из вершины В к основанию АD
АВН- прямоугольный треугольник, а в прямоугольном треугольнике сторона ВН, лежащая на против угла в 30 градусов= половине гипотенузы АВ
ВН=6/2=3
3.т.к ABCD- паралелограмм, следовательно BC=AD
S(площадь паралелограмма) ABCD=ВН*АD
S=3*8=24см_2