Ответы
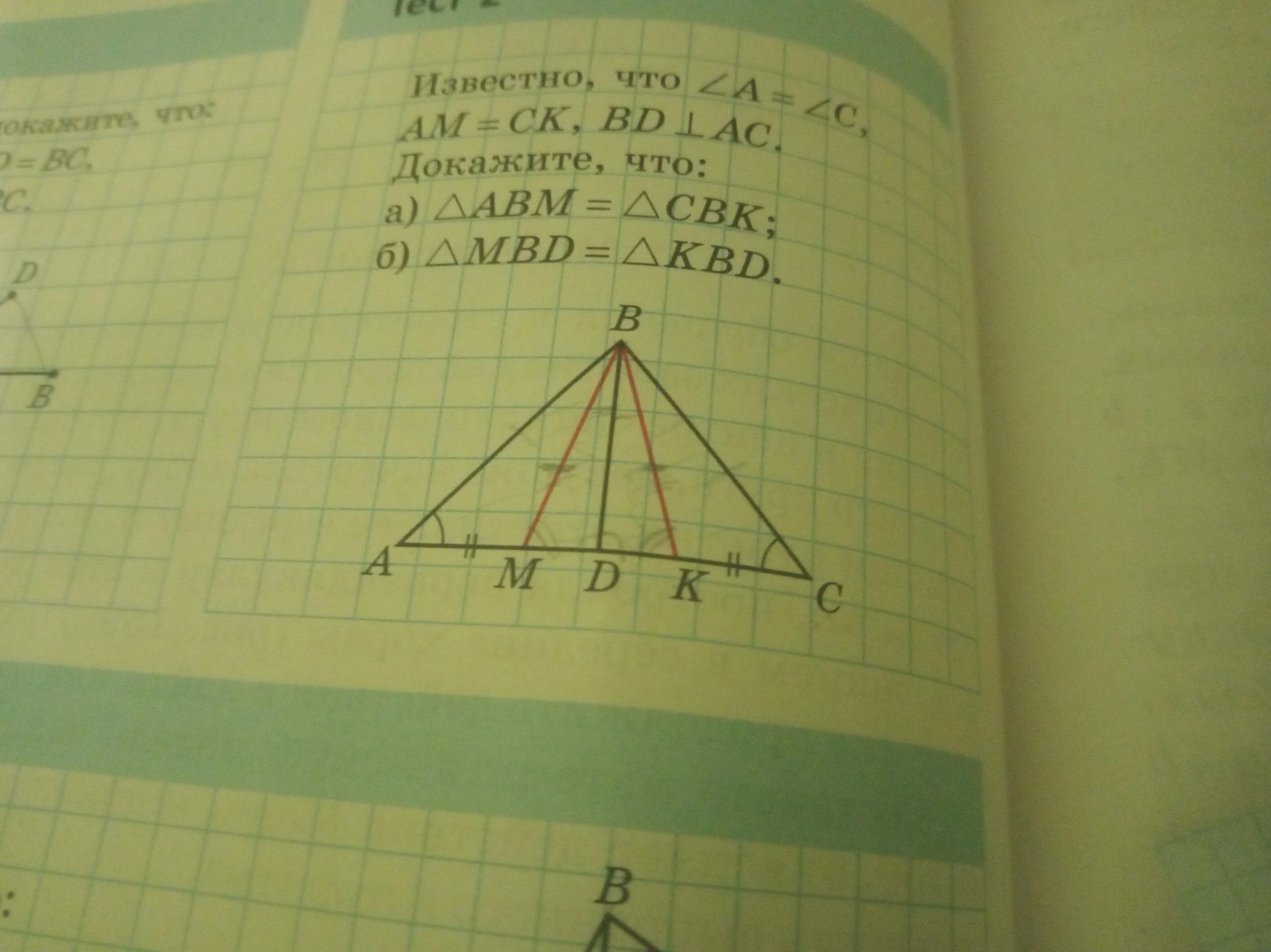
а) Высота равнобедренного треугольника - это перпендикуляр. А значит АВ=СВ, АВМ=СВК по первому признаку равенства треугольников.
б) если АМ=СК, то МD=DK, BD перпендикуляр так мы знаем что угол D= 90° и равен для обоих треугольников. МВD=KBD по первому признаку равенства треугольников
Ответ:
Объяснение:
Так как углы А и С равны то треугольник АВС равнобедренный. Из этого следует АВ=ВС. Отсюда треугольники АВМ=СВК по двум сторонам и углу между ними (ВА=ВС, АМ=СК угол А=углу С).
Если ВД перпендикулярен АС то он перпендикулярен МК. ВМ=ВК (из равенства треугольников АВМ и СВК. Из равенства сторон ВМ=ВК получаем что треугольник МВК равнобедренный. Высота ВД (ВД перпендикулярен МК) проведенная из вершины равнобедренного треугольника к его основанию делит основание треугольника МВК на две равные части МД=ДК. Отсюда треугольники МВД и КВД равны по трем сторонам (ВМ=ВК, МД=ДК, ВД общая)