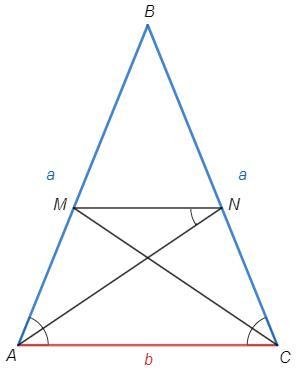
В равнобедренном треугольнике АВС известны стороны AB =ВС= a, АС= b. Отрезки AN и CM – биссектрисы углов А и
С. Найдите длины отрезков MN, AM, MB
СРОЧНО
Ответы
Ответ дал:
4
Биссектриса (CM) треугольника делит противоположную сторону (AB) на части, пропорциональные прилежащим сторонам.
AM/BM =AC/BC =b/a (по теореме о биссектрисе)
Пусть AM=bx, BM=ax
AB=AM+BM => a =bx+ax =x(a+b) => x=a/(a+b)
AM =ab/(a+b)
BM =a^2/(a+b)
△MAC=△NCA (по общей стороне и прилежащим углам) =>
высоты из M и N равны => MN||AC
∠MNA =∠CAN (накрест лежащие) =∠MAN =>
△AMN - равнобедренный, MN=AM =ab/(a+b)
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
AM=bx, MB=ax
AB=AM+MB => a=(b+a)x => x=a/(a+b)