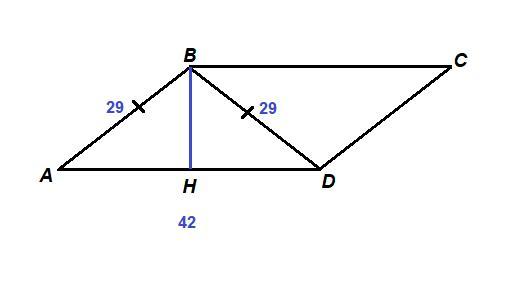
Одна из сторон параллелограмма ABCD равна диагонали BD, длина которой 29 см, сторона AD равна 42 см. Найдите площадь параллелограмма. *
5 points
Ответы
Ответ дал:
5
Ответ:
840 см²
Объяснение:
AB = BD, значит ΔABD равнобедренный с основанием AD.
Проведем ВН - высоту ΔABD, она является медианой, значит
АН = 1/2 AD = 1/2 · 42 = 21 см
Из прямоугольного треугольника ABH по теореме Пифагора:
см
ВН является и высотой параллелограмма.
Площадь параллелограмма:
S = AD · BH = 42 · 20 = 840 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад