Вынесите множитель из-под знака корня:
1) √(14x^2 ), если x ≤ 0;
2) √(125x^12 );
3) √(-y^3 ).
ЗА ПОМОЩЬ 50 баллов.
Ответы
Ответ дал:
12
Ответ и Объяснение:
Полное условие приведено в приложенном рисунке.
Так как
то:
Приложения:
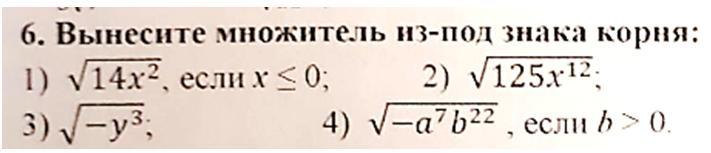
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад