Докажите, что диагонали квадрата являются биссектрисами его углов. (По определению, у квадрата все
стороны равны, а все углы – прямые).
Ответы
Ответ дал:
13
Объяснение:
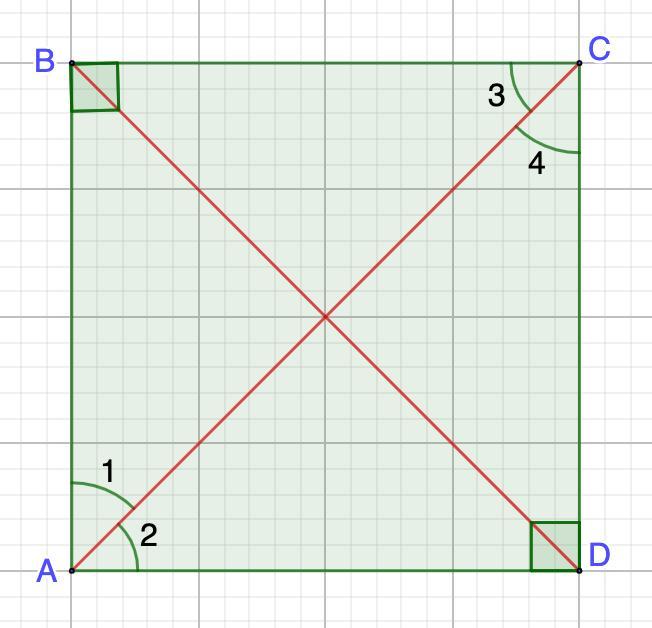
Дано: ABCD - квадрат;
∠A = ∠B = ∠C = ∠D = 90°
AB = BC = CD = AD
AC и BD - диагонали.
Доказать: AC и BD - биссектрисы
Доказательство:
Рассмотрим ΔABC и ΔACD - прямоугольные;
AB = BC = CD = AD (условие)
⇒ ΔABC = ΔACD (по двум катетам)
- В равных треугольника соответственные элементы равны.
⇒ ∠1 = ∠2 ; ∠3 = ∠4
⇒ АС - биссектриса углов ∠А и ∠С.
Аналогично доказывается, что BD - биссектриса ∠B и ∠D.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад