Предмет: Геометрия
Автор: rerihrobert4
Вопрос задан 2 года назад

Даны две скрещивающиеся прямые, расстояние между которыми равно 10. Прямая l пересекает две параллельные плоскости, проходящие соответственно через данные скрещивающиеся прямые, в точках A и B. Если угол между прямой l и ее проекциями на этих плоскостях равен 30°, найди длину отрезка AB.

4585o7k5099: две скрещивающиеся прямые лежат в двух параллельных плоскостях, скрещиваются, и расстояние равно 10 то есть прямая перпендикулярна двум плоскостям и равна 10 прямая l это наклонная с основанием 30 градусов можно так составить прямоугольный треугольник и решить , гипотенуза равна катету умноженному на 2 напротив угла 30 градусов 10*2=20

Ответы

Ответ дал: ReMiDa

Ответ:

20 ед.

Объяснение:

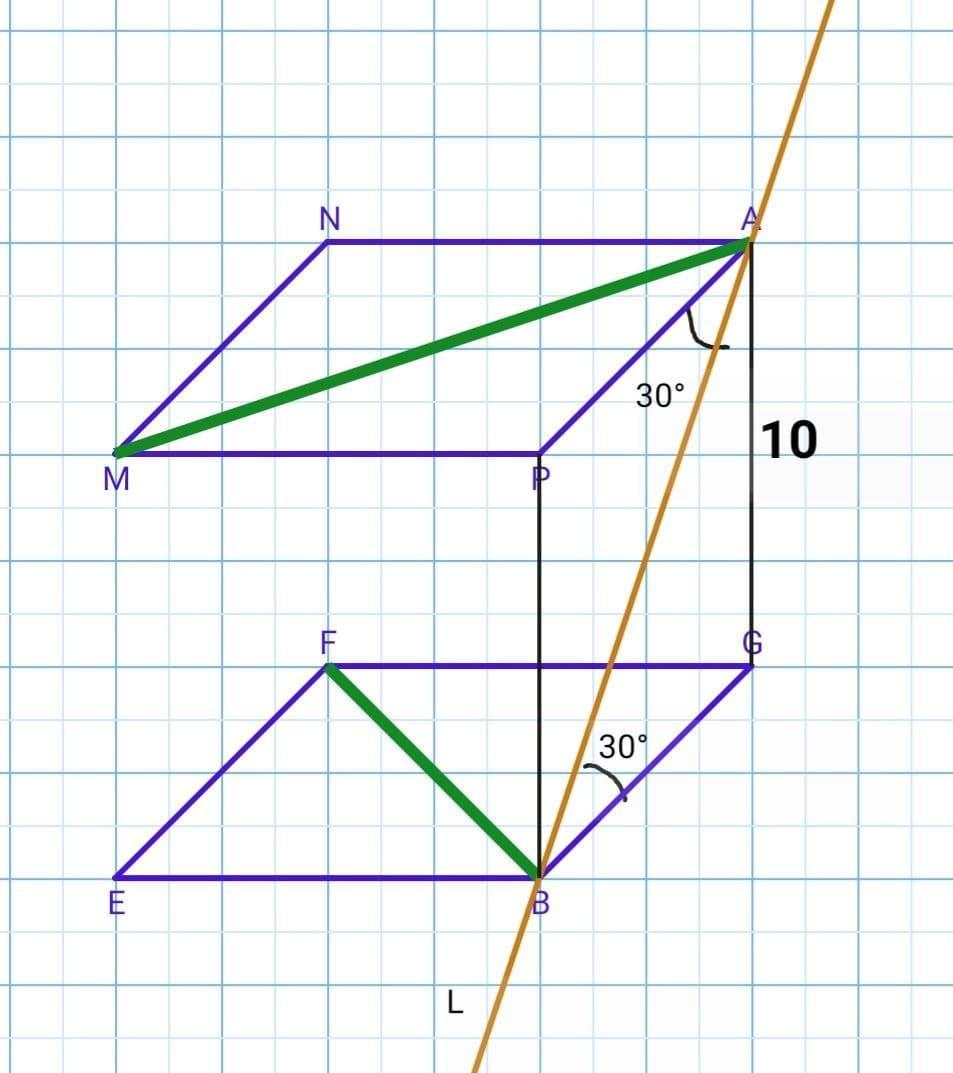
АМ и BF - скрещивающиеся прямые.

АМ ∈ (MAP), BF∈ (EGB),

A, B ∈ L

L∩(MAP)=A, B∩(EGB)=B

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Расстоянием между скрещивающимися прямыми называют расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую.

Плоскости (MAP) и (EGB) - параллельны. AG ⊥ (MAP), AG ⊥ (EGB). Расстояние (перпендикуляр) между этими плоскостями и будет расстоянием между прямыми: AG = 10

BG - проекция прямой L на плоскость (EGB), ∠АGB= 30°

AP - проекция прямой L на плоскость (МAP), ∠ВAP= 30°

ΔАВG (∠G=90°). Катет, лежащий против угла в 30° равен половине гипотенузы: АВ = 2*АG=2*10=20

Приложения: