Ответы
Ответ дал:
3
решение на фото
..................
Приложения:
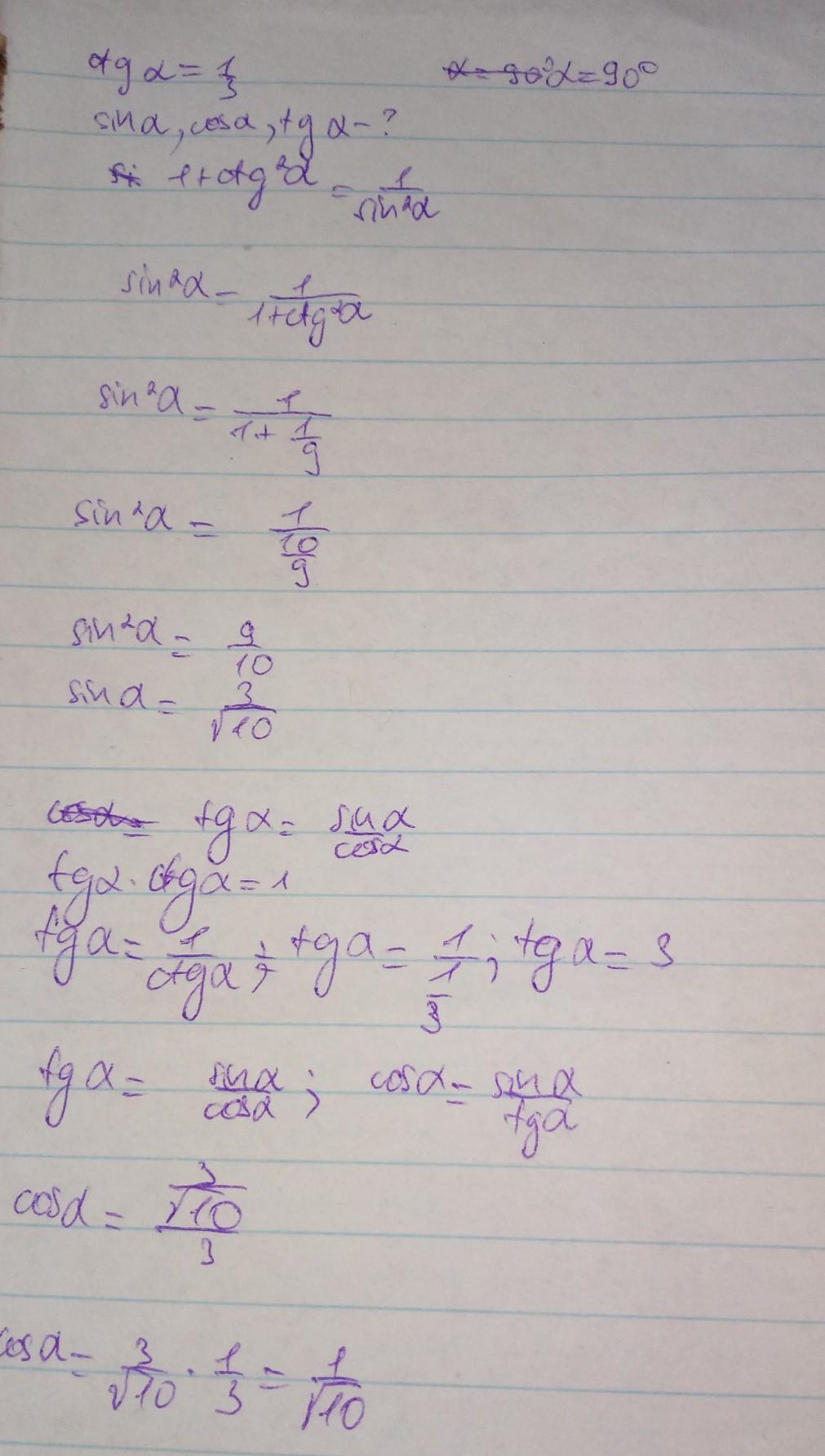
6yTep6pog:
Спасибо что не остались в стороне и помогли с заданием!❤️
почерк непонятный
помогите пожалуйста,с последним заданием, геометрия,у меня на аккаунте,прошу
Ответ дал:
5
Ответ:
Спасибо большое!
Это правильно??
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад