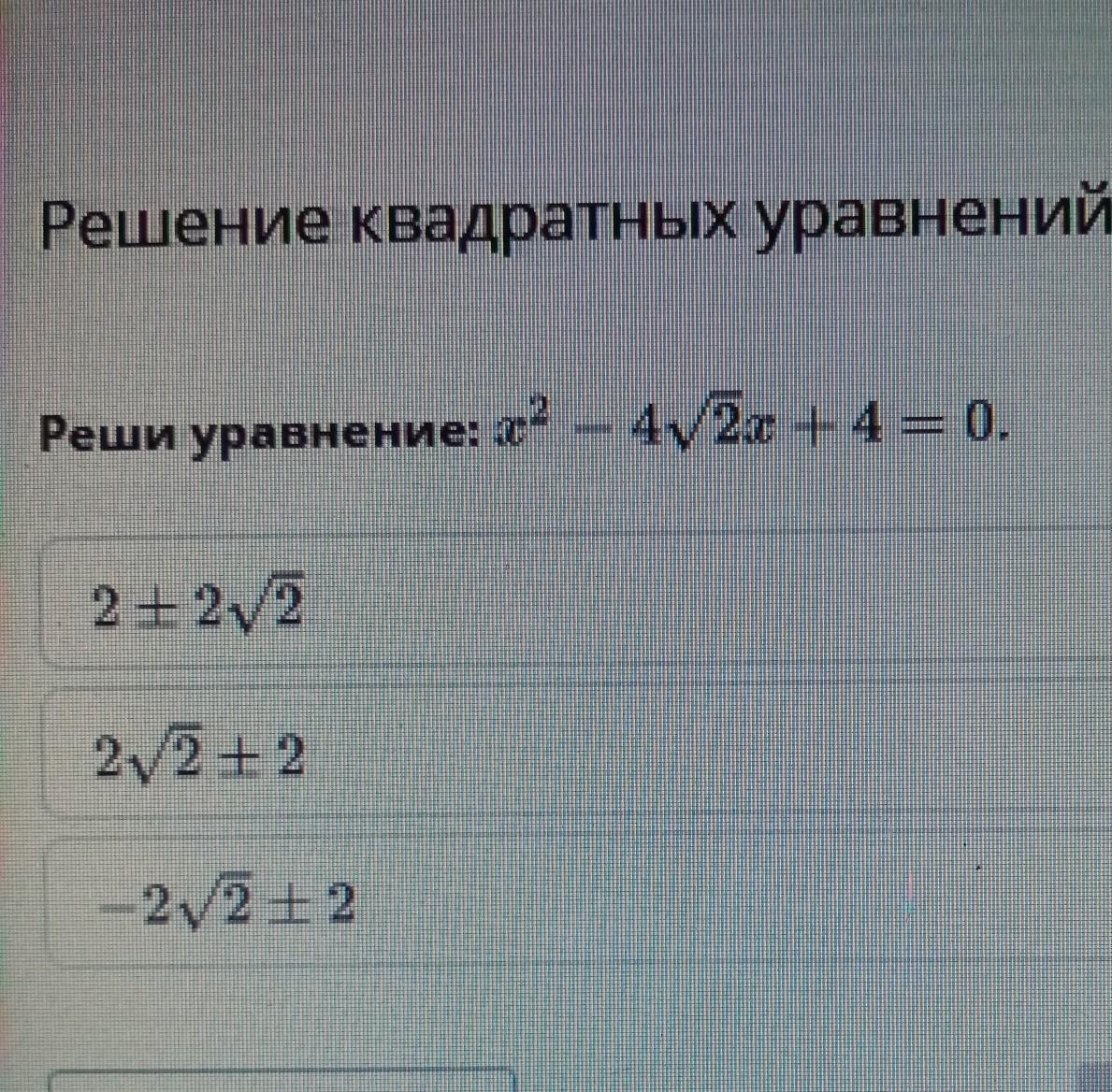
Ответы
Ответ дал:
2
Ответ:
Объяснение:
Данное уравнение является квадратным вида:
Найдем дискриминант.
.
Корни уравнения найдем по формуле.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад