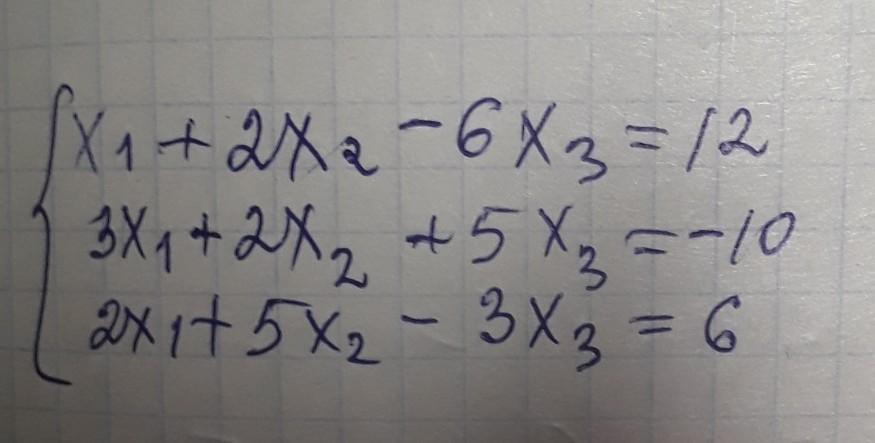Question

Даю 30 Баллов! Решить систему уравнений Методом Гаусса И Крамера!​

Answer 1

Решение методом Крамера.

x1        x2       x3      B  -59

1          2         -6      12 Определитель

3         2         5       -10  

2         5       -3         6  

Заменяем 1-й столбец на вектор результатов B:    

12         2        -6          0

-10        2         5        Определитель

6          5         -3  

Заменяем 2-й столбец на вектор результатов B:    

1            12        -6     0

3         -10          5  Определитель

2          6           -3  

Заменяем 3-й столбец на вектор результатов B:    

1     2           12  118

3          2          -10  Определитель

2         5            6  

x1= 0 / -59 = 0  

x2= 0 / -59 = 0  

x3= 118 / -59 = -2.  

Определитель проще всего находить по схеме Саррюса или параллельных полосок.

Первые два столбца матрицы записываются справа возле матрицы. Произведения элементов, стоящих по диагонали направо вниз, складываются, затем из результата вычитаются произведения элементов, находящихся на линиях налево вниз.

Вот пример первого.

1         2       -6|      1       2

3        2        5|      3       2

2        5       -3|       2       5  =

   

= -6 +20 -90+18 -25+ 24 = -59.