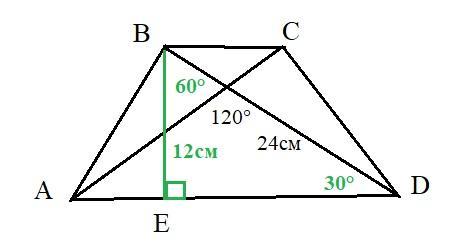
В равнобедренной трапеции угол между диагоналями, лежащий против основания, равен 120°. Найдите высоту трапеции, если длина диагонали равна 24 см.
Ответы
Ответ дал:
1
Ответ: 12 см.
Объяснение:
ABCD - трапеция BE - высота. Точка О - точка пересечения диагоналей.
∠AOD=D=BOC=120°;
∠COB=∠BCO=(180°-120°)/2=30°.
Из ΔBDE ∠ DBE=60° (90°-30°=60°); Тогда ∠BDE=180°-(60°+90°)=30°.
Высота ВЕ=BD*Sin30°=24*1/2=12 см.
Приложения:
theden966:
спасибо)
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад