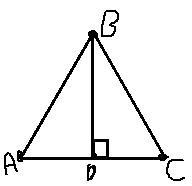
В треугольнике АВС проведена медиана ВD. Медиана ВD перпендикулярна стороне АС. Докажите, что треугольник АВС – равнобедренный
в файле есть еще задания
Приложения:
101100101:
с чертежом дольше... надо?
Ответы
Ответ дал:
1
Дано:
ABC - треугольник.
BD - медиана
BD ⊥ AC
Доказать: ABC - равнобедренный
1) Т.к BD-медина, перпендикулярная AC, то она является высотой.
2) Т.к BD- медиана и высота, то по утверждению "В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой" треугольник ABC равнобедренный, что и требовалось доказать.
Приложения:
можешь помочь с заданиями которые в файле можно и без чертежа
ок
решение в файле
спасибо
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад