17.14. Пирамида Хеопса имеет форму правильной четырехугольной пирамиды, сторона основания которой равна 230 м, а высота около 138 м. Найдите тангенс двугранного угла, образованного боковой гранью и основанием этой пирамиды. Используя таблицу тригонометрических функций, найдите приближенное значение этого угла.
Ответы
Ответ дал:
0
Ответ:
≈ 50°12'
Объяснение:
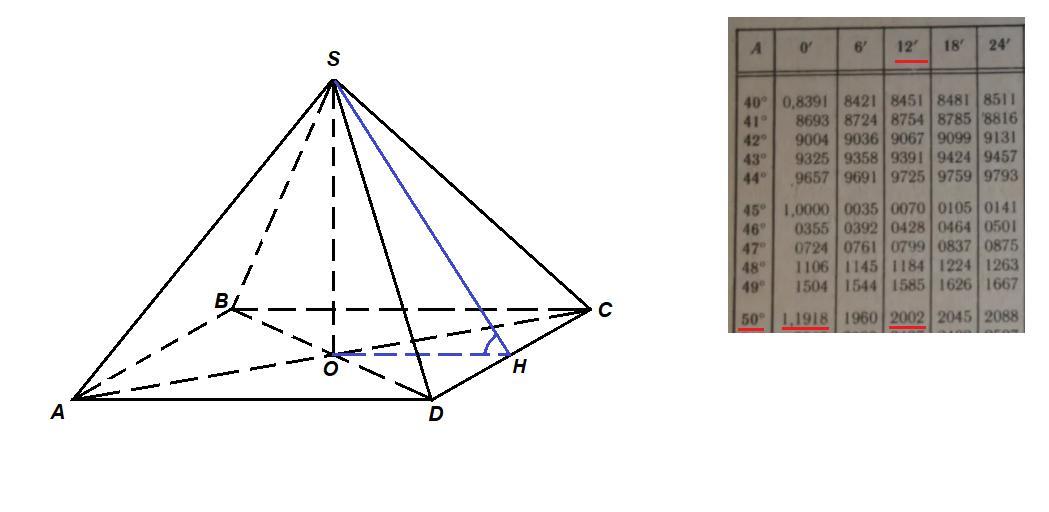
Пусть Н - середина CD.
Тогда ОН⊥CD как медиана и высота равнобедренного треугольника OCD (OC = OD по свойству диагоналей квадрата),
СН⊥CD как медиана и высота равнобедренного треугольника CSD,
значит, ∠SHO - линейный угол двугранного угла, образованного боковой гранью пирамиды и основанием, - искомый.
О - середина АС по свойству диагоналей квадрата, тогда ОН - средняя линия ΔACD,
ОН = AD : 2 = 230 : 2 = 115 м
ΔSHO:
∠SOH ≈ 50°
или точнее ∠SOH ≈ 50°12'
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад