Question

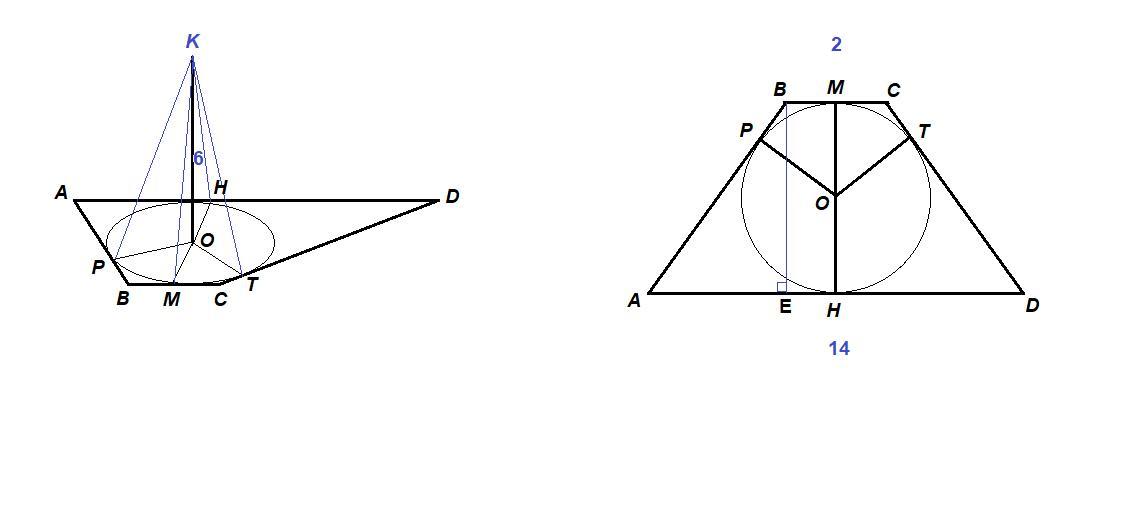
Основи рівнобічної трапеції дорівнюють 2 см і 14 см . Через центр О кола , вписано в цю трапецію, проведено перпендикуляр ОК до площини трапеції , ОК-6см. Знайдіть відстань від точки К до сторін трапеції .

БУДЬ ЛАСКА ДОПОМОЖІТЬ 30 баллов ​

Answer 1

Ответ:

$\sqrt{43}$  см

Объяснение:

Проведем радиусы в точки касания окружности со сторонами трапеции.

ОР⊥АВ, ОМ⊥ВС, ОТ⊥CD, OH⊥AD по свойству касательной.

ОР - проекция КР на плоскость (АВС), значит КР⊥АВ по теореме о трех перпендикулярах.

Аналогично, КМ⊥ВС, КТ⊥CD, KH⊥AD, значит

КР, КМ, КТ, КН - искомые расстояния от точки К до сторон трапеции.

ΔКОР = ΔКОМ = ΔКОТ = ΔКОН по двум катетам:

• треугольники прямоугольные, так как ОК⊥(АВС);
• ОР = ОМ = ОТ = ОН как радиусы;
• КО - общий катет.

⇒  КР = КМ = КТ = КН.

Если в четырехугольник вписана окружность, то суммы противолежащих сторон равны:

AB + CD = AD + BC = 14 + 2 = 16 см

Так как трапеция равнобедренная, то

АВ = CD = 16 : 2 = 8 см

BE - высота трапеции.

По свойству равнобедренной трапеции:

$AE=\dfrac{AD - BC}{2}=\dfrac{14-2}{2}=6$ см

Из прямоугольного треугольника АВЕ по теореме Пифагора:

$BE=\sqrt{AB^2-AE^2}=\sqrt{8^2-6^2}=\sqrt{64-36}=\sqrt{28}=2\sqrt{7}$ см

ОМ = 0,5 · ВЕ = 0,5 · 2√7 = √7 см

ΔКОМ:  ∠КОМ = 90°, по теореме Пифагора

  $KM=\sqrt{KO^2+OM^2}=\sqrt{6^2+(\sqrt{7})^2}=$

   $=\sqrt{36+7}=\sqrt{43}$ см